Question

A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram’s base is the side of the triangle with 28 cm. Find the height of the parallelogram.

Answer 1

Hint: Use Heron’s formula to find the area of the given triangle. According to Heron’s formula,
if a, b and c are the sides of a triangle and ‘s’ is the semi-perimeter of the triangle, then,
$s=\dfrac{a+b+c}{2}$
Area of the triangle$=\sqrt{s(s-a)(s-b)(s-c)}$
Area of a parallelogram= Base$\times $ height
Equate the area of the triangle with that of the parallelogram to find the unknown height of the parallelogram. Draw figures for ease in visualizing the question.

Complete step by step answer:
We are given the sides of a triangle. We are also given that the area of the triangle is the same as that of the parallelogram and that the base of the parallelogram coincides with the side of the triangle which is equal to 28 cm. We are asked to find the height of the parallelogram.
According to the question, the triangle and parallelogram would look like,

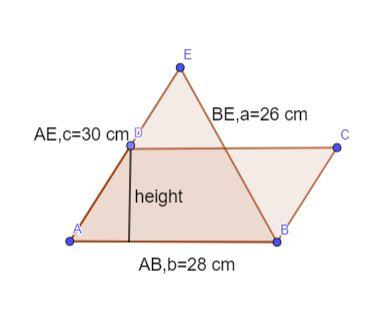
The semi-perimeter of the triangle, $s=\dfrac{a+b+c}{2}$
$=\dfrac{26+28+30}{2}$
$=\dfrac{84}{2}=42\,cm$
Using Heron’s formula,
Area of the triangle$=\sqrt{s(s-a)(s-b)(s-c)}$
$=\sqrt{42(42-26)(42-28)(42-30)}$
$=\sqrt{42\times (16)\times (14)\times (12)}$
$=\sqrt{42\times (16)\times (14)\times (12)}$
$=\sqrt{7\times 6\times 4\times 4\times 7\times 2\times 2\times 6}$
\[=7\times 6\times 4\times 2\]
$=336\,c{{m}^{2}}$
$\therefore $ Area of the triangle$=336\,c{{m}^{2}}$
We are given that area of the triangle is equal to the area of the parallelogram and we know that area of a parallelogram is equal to Base$\times $ height.
Hence,
Area of the parallelogram$=336\,c{{m}^{2}}$
Base$\times $ height$=336\,c{{m}^{2}}$
We are given that the base of the parallelogram coincides with the side of the triangle which is equal to 28 cm.
28 cm $\times $ height$=336\,c{{m}^{2}}$
$\therefore $Height of the parallelogram$=\dfrac{336\,c{{m}^{2}}}{28\,cm}=12\,cm$
Hence, the height of the parallelogram is equal to 12 cm.

Note:
Keep every measurement in the same unit. If the units differ, make necessary conversions. While finding the area of the triangle using Heron’s formula, rather than directly taking the root using the long division method, look for chances of simplification.
The semi-perimeter of the triangle is simply half the perimeter of the triangle.