Question

A triangle ABC is right angled at A. AL is drawn perpendicular to BC. Prove that \[\angle BAL=\angle ACB\].

Answer 1

Hint: First of all we will suppose \[\angle BAL\] and \[\angle ACB\] to be a variable and then we will use the property of a triangle that sum of the interior angles of a triangle is equal to \[{{180}^{\circ }}\].

Complete step-by-step answer:
We have been given a triangle ABC right angled at A and AL is drawn perpendicular to BC. Then we have to prove that \[\angle BAL=\angle ACB\].

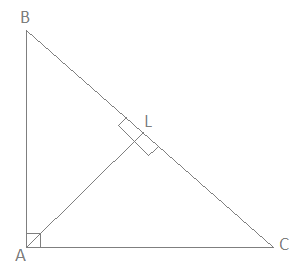
Let us suppose \[\angle BAL=x\] and \[\angle ACB=y\]
In \[\Delta ABL\],
\[\angle BAL={{90}^{\circ }}-\angle ABC\]
Since \[\Delta ABL\] is right angled at L
\[\Rightarrow x={{90}^{\circ }}-\angle ABC....(1)\]
Once again, in \[\Delta ABC\],
\[\angle ABL+\angle ACB+\angle BAC={{180}^{\circ }}\]
Since triangle ABC is right angled at A, we have,
\[\angle BAC={{90}^{\circ }}\]
\[\angle ABL+\angle ACB+{{90}^{\circ }}={{180}^{\circ }}\]
\[\angle ABL+\angle ACB={{90}^{\circ }}\]
\[\begin{align}
  & \Rightarrow \angle ABC+y={{90}^{\circ }} \\
 & \Rightarrow y={{90}^{\circ }}-\angle ABC.....(2) \\
\end{align}\]
On comparing the equation (1) and (2), we find that the right hand side of equation (1) and (2) are equal.
So, the left hand side must be equal.
\[\begin{align}
  & \Rightarrow x=y \\
 & \Rightarrow \angle BAL=\angle ACB \\
\end{align}\]

Note: Remember the property of a triangle is that the sum of the interior angles of any triangle is equal to \[{{180}^{\circ }}\]. Also, remember that a right angled triangle means at least one angle of a triangle measures \[{{90}^{\circ }}\]. Hence the sum of the other two angles of a triangle is equal to \[{{90}^{\circ }}\]. Perpendicular means a line or a plane that is at \[{{90}^{\circ }}\] to the other line or a plane respectively.