Question

A train starts at 8 O’ clock and moves eastward at the speed of 60 km/h. Another train starts from the same point at 9 O’ clock and travels southward at the speed of 80 km/h. Find the rate at which they are moving away from each other at 12 O’ clock.

Answer 1

Hint: Here, we will first find the positions of both the trains at 12 O’ clock and find the distance between them at 12 O’ clock. Establish a relation between known quantities and unknown quantities and find the speed at particular time using differentiation.

Complete step by step answer:
Given, speed along eastward direction, i.e. along x-axis, $dx = 60$ km/h.
Also, given speed along southward direction, i.e. along negative y-axis, $dy = 80$ km/h.

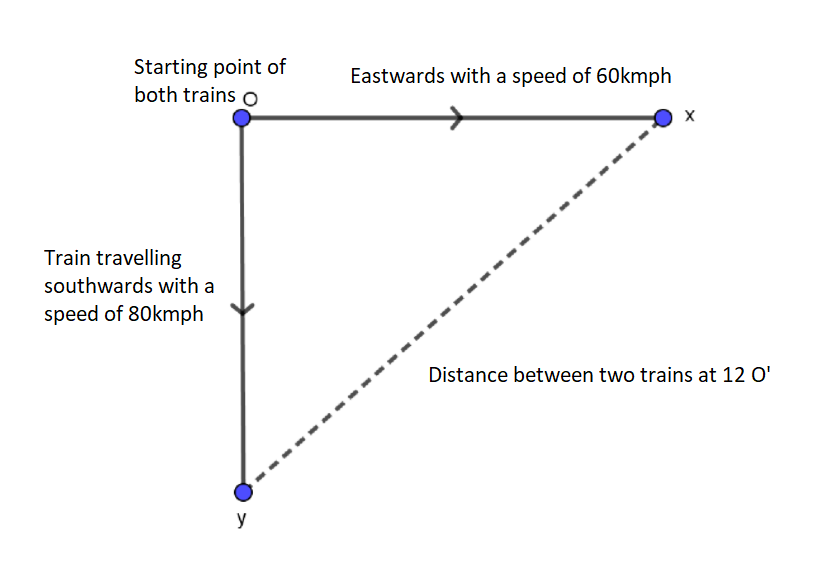
Time taken by train moving towards eastward direction to reach a particular point at 12 O’ Clock = 12 O’ clock – 8 O’ clock = 4 hours
Distance covered by train in eastward direction in 4 hours i.e. train position at 12 O’ clock from initial position, $x = 60 \times 4 = 240$km.
And, time taken by train moving towards southward direction to reach a particular point at 12 O’ Clock = 12 O’ clock – 9 O’ clock = 3 hours
Distance covered by train in southward direction in 3 hours i.e. train position at 12 O’ clock from initial position, \[y = 80 \times 3 = 240\]km.
Distance between two trains at 12 O’ clock, $z = \sqrt {{x^2} + {y^2}} $ …(i)
Z at 12 O’ clock = $\sqrt {{{\left( {240} \right)}^2} + {{\left( {240} \right)}^2}} = \sqrt {57600 + 57600} $
= $\sqrt {114200} = 240\sqrt 2 $ km
Squaring both sides of equation (i), we get
${z^2} = {x^2} + {y^2}$
Differentiating both sides,
$2zdz = 2xdx + 2ydy$
$ \Rightarrow dz = \dfrac{{2xdx + 2ydy}}{{2z}}$
We have at 12 O’ clock, $x = 240,dx = 60,y = 240,dy = 80,z = 240\sqrt 2 $
Putting values in equation (ii), we get
$dz = \dfrac{{2 \times 240 \times 60 + 2 \times 240 \times 80}}{{2 \times 240\sqrt 2 }}$
$ \Rightarrow dz = \dfrac{{28800 + 38400}}{{480\sqrt 2 }}$
$ \Rightarrow dz = \dfrac{{67200}}{{480\sqrt 2 }} = \dfrac{{140}}{{\sqrt 2 }} = 70\sqrt 2 $

Therefore, the rate at which the two trains are moving away from each other at 12 O’ clock is $70\sqrt 2 $ km/h.


Note:
In these types of questions, drawing the figure to understand the relative position, appropriate diagram will help in finding the relative distance between the trains/cars at a particular time. Use differentiation methods to find the speed at a particular time.