Question

A train 75m long overtook a person who was walking at the rate of 6km/hr and passed him in $ 7\dfrac{1}{2} $ seconds. Subsequently it overtook a second person and passed him in $ 6\dfrac{3}{4} $ seconds. At what rate was the second person travelling?
a. 4 km/hr
b. 1 km/hr
c. 2 km/hr
d. 5 km/hr

Answer 1

Hint: We will use the concept of relative speed here. According to the relative speed if both the objects are moving in the same direction, then the net speed will be given by subtracting their speeds, whereas if both the objects are moving in opposite directions, then their speeds will be added. We will also use the formula, $ \text{speed=}\dfrac{\text{distance}}{\text{time}} $ and calculate the speed of the train in two different cases and find the speed of the second person accordingly.

Complete step-by-step answer:
It is given in the question that, a train 75m long overtook a person who was walking at the rate of 6km/hr and passed him in $ 7\dfrac{1}{2} $ seconds. Subsequently it overtook a second person and passed him in $ 6\dfrac{3}{4} $ seconds. And we have been asked to find the rate at which the second person was travelling.
As the length of the train is 75m, the distance covered by the train to overtake a person will also be 75m.

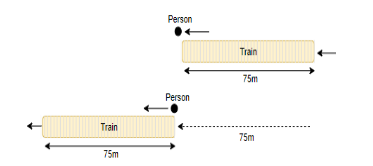
We will first consider the case of the first person.
We have been given the time as $ 7\dfrac{1}{2} $ . So, we can first convert the mixed fraction, $ 7\dfrac{1}{2} $ into normal fraction by multiplying 7 with 2 and then adding 1 to it. So, we will get,
 $ 7\dfrac{1}{2}=\dfrac{\left( 7\times 2 \right)+1}{2}=\dfrac{14+1}{2}=\dfrac{15}{2} $
Now, we will find the speed of the train relative to the first person. We know that $ \text{speed=}\dfrac{\text{distance}}{\text{time}} $ . So, the distance to be covered by the train is 75m and the time taken by the train to overtake the first person will be $ \dfrac{15}{2} $ seconds. So, we get,
 $ \begin{align}
  & \text{speed=}\dfrac{\text{distance}}{\text{time}}=\dfrac{75}{\dfrac{15}{2}} \\
 & =\dfrac{75\times 2}{15} \\
 & =\dfrac{150}{15} \\
 & =10m/s \\
\end{align} $
Now, 10 m/s can be converted into km/hr, by multiplying it with $ \dfrac{18}{5} $ , so we get the relative speed of train with respect to the first person as,
 $ 10m/s=10\times \dfrac{18}{5}=36km/hr $
We have been given that the first person is walking at the rate of 6km/hr in the same direction as that of the train. We know that this is a case of relative motion.
So, in relative motion if both the objects are moving in the same direction, then the net speed will be given by subtracting their speeds, whereas if both the objects are moving in opposite directions, then the net speed will be given by the addition of their speeds.
Now, let us assume the speed of the train as x km/hr. So, in case of the first person, we know that both the person and the train are moving in the same direction, so subtraction will take place.Thus, (x-6) must be equal to 36 km/hr. So, we can write,
(x - 6) = 36
On transposing -6 from LHS to RHS, we get,
x = 36 + 6
x = 42 km/hr
It means that the speed of the train is 42 km/hr.
Now, next we are given that the train crosses the second person in $ 6\dfrac{3}{4} $ seconds, so we will first convert the mixed fraction $ 6\dfrac{3}{4} $ to the normal fraction, so we get,
 $ 6\dfrac{3}{4}=\dfrac{\left( 6\times 4 \right)+3}{4}=\dfrac{27}{4} $
Now, the relative speed of the train with respect to the second person will be found using the formula, $ \text{speed=}\dfrac{\text{distance}}{\text{time}} $ . Here, the distance is 75m and the time is $ \dfrac{27}{4} $ seconds. So, we get the relative speed of the train with respect to the second person as,
 $ \begin{align}
  & \text{speed=}\dfrac{\text{distance}}{\text{time}}=\dfrac{75}{\dfrac{27}{4}} \\
 & =\dfrac{75\times 4}{27} \\
 & =\dfrac{100}{9}m/s \\
\end{align} $
Now, $ \dfrac{100}{9}m/s $ can be converted into km/hr, by multiplying it with $ \dfrac{18}{5} $ , so we get the relative speed of train with respect to the second person as,
 $ \dfrac{100}{9}m/s=\dfrac{100}{9}\times \dfrac{18}{5}=40km/hr $
Now, let us assume the speed of the second person as y km/hr.
Thus, the relative speed will be (42-y), as both the train and the person are moving in the same direction. Also, we know that the relative speed of the train with respect to the second person is 40 km/hr. So, we can write,
(42 - y) = 40
On transposing 42 from LHS to the RHS, we get,
- y = 40 - 42
- y = - 2
On multiplying both the sides by -1, we get,
y = 2
Therefore, the speed of the second person is equal to 2 km/hr.
So, the correct answer is “Option C”.

Note: Most of the students make mistakes by calculating the relative speed of the train in m/s and the speed of the person in km/hr. And due to two different units, the whole calculation will become wrong. So, it is highly recommended that the students convert all the values in the same unit. Also, in case of the second person, some students may write the relative speed as (y - 42) instead of (42 - y) and will get the wrong answer, so the students must be careful while solving this question and should do the calculations step by step in order to avoid any mistakes.