Question

A tower stands at the center of a circular park. A and B are two points of the boundary of the park such that AB (=a) subtends an angle ${60^0}$ at the foot of the tower, and the angle of elevation of the top of the tower from A or B is ${30^0}$ . The height of the tower is
\[
  A.{\text{ }}\dfrac{{2a}}{{\sqrt 3 }} \\
  B.{\text{ }}2\sqrt 3 a \\
  C.{\text{ }}\dfrac{a}{{\sqrt 3 }} \\
  D.{\text{ }}a\sqrt 3 \\
 \]

Answer 1

Hint: In order to find the height of the tower first make the diagram with the help of given statement, with the help of diagram it will be more clear about the positions of different point and the pole in the park , then we will proceed further by using tangent formula in a right angle triangle formed by the pole.

Complete step-by-step answer:
We will solve the problem with the help of a given figure.

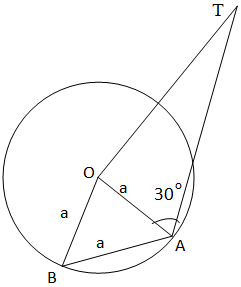
For the given problem let OT is the tower that makes an angle of ${30^0}$ with the points A and B respectively and ${60^0}$ at the foot of the tower.
So the angle $\angle OAT = {30^0}$
As the sides of triangle OAB are same as AB=a
So triangle OAB is an equilateral triangle.
So, OA = a
Also the pole makes ${60^0}$ with the base and ${30^0}$ with the end points
So, in triangle AOT
$
  \angle TOA = {60^0} \\
  \angle OAT = {30^0} \\
  \therefore \angle ATO = {180^0} - \angle TOA - \angle OAT \\
   \Rightarrow \angle ATO = {180^0} - {60^0} - {30^0} \\
   \Rightarrow \angle ATO = {90^0} \\
 $
So the given triangle AOT is right angled at point T.
Now let us use the formula for tangent of angle for the right angled triangle to find the relation between the height of the pole “h” and the side “a” of the triangle or the distance between the pole and outer point.
So for right triangle ATO
$
  \tan \angle OAT = \dfrac{h}{a} \\
   \Rightarrow \tan {30^0} = \dfrac{h}{a} \\
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{a}{\text{ }}\left[ {\because \tan {{30}^0} = \dfrac{1}{{\sqrt 3 }}} \right] \\
   \Rightarrow \dfrac{a}{{\sqrt 3 }} = h \\
   \Rightarrow h = \dfrac{a}{{\sqrt 3 }} \\
 $
Hence, the height of the pole is $\dfrac{a}{{\sqrt 3 }}$
So, option C is the correct option.


Note- In order to solve such problems related to heights and distances, students must start with the diagram of the problem and should try to find the angles by the help of figures in order to use trigonometric formulas and values. Students must remember the values of trigonometric functions for some common trigonometric angles.