Question

A tower 51mts high has a mark at a height of \[25\] mts from the ground. At what distance the two parts subtend equal angle to an eye at the height of \[5\] mts from the ground
A. $20mts$
B. $30mts$
C. $15mts$
D. $160mts$

Answer 1

Hint: We will make a given diagram according to the given information in the question .Then we will take two triangles separately and find a side by using Pythagora's theorem.

Complete step-by-step answer:

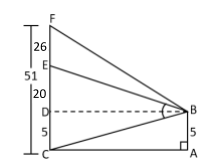
Here, $CF$ is the height of the tower and it has a mark at height of $25$meters from the ground.
$AB = CD = 5\,meters,\,\,DE = 2\,meters$
$
  DE = EC - CD \\
  DE = 25 - 5 \\
  DE = 20meters \\
 $
$CF = 51\,meters$
$
  DF = DE + EF \\
  DF = 20 + 26 \\
  DF = 46meters \\
 $
Now, according to the question:
$\angle FBE = \angle EBC$ ($\because $given)
$\therefore BE$ is the bisector of $\angle CBF$ and as such it divides the base $CF$ in the ratio of the arm of the angle. Then by the angle bisector theorem .
$\dfrac{{BC}}{{BF}} = \dfrac{{CE}}{{EF}}$ …..(i)
Now, In $\Delta BDE,$ at point $D = {90^o}$
By using Pythagoras theorem, we have
(Hypotenuse)2 = (base)2+(perpendicular)2
${(BF)^2} = {(BD)^2} + {(DF)^2}$
${(BF)^2} = {(BD)^2} + {(DF)^2}$
We will substitute the value of DF,$DF = 46$
$
  {(BF)^2} = {(BD)^2} + {(46)^2} \\
   \Rightarrow BF = \sqrt {{{(D)}^2} + {{(46)}^2}} \\
 $
In $\Delta BCD$at point Dis$90$, so by using Pythagoras theorem, we have
(Hypotenuse)2 = (base)2+(perpendicular)2
\[{(BC)^2} = {(BD)^2} + {(DC)^2}\]
$BC = \sqrt {{{(BD)}^2} + {{(DC)}^2}} $
We will substitute the value of DC,$DC = 5$
$BC = \sqrt {{{(BD)}^2} + {{(5)}^2}} $
Now, we will put the value of $BF$and $BC$ in equation (i) ,we have
$\dfrac{{\sqrt {{{(BD)}^2} + {{(5)}^2}} }}{{\sqrt {{{(BD)}^2} + {{(46)}^2}} }} = \dfrac{{CE}}{{EF}}$
Squaring both sides, we will get
$\dfrac{{{{\left( {\sqrt {{{(BD)}^2} + {{(5)}^2}} } \right)}^2}}}{{{{\left( {\sqrt {{{(BD)}^2} + {{(46)}^2}} } \right)}^2}}} = {\left( {\dfrac{{CE}}{{EF}}} \right)^2}$
\[\dfrac{{{{(BD)}^2} + {{(5)}^2}}}{{{{(BD)}^2} + {{(46)}^2}}} = {\left( {\dfrac{{25}}{{26}}} \right)^2}\]
$\dfrac{{{{(BD)}^2} + 25}}{{{{(BD)}^2} + 2116}} = \dfrac{{625}}{{676}}$
$676[{(BD)^2} + 25] = 625[{(BD)^2} + 2116]$
We will equate the values of ${(BD)^2}$, we have
\[676{(BD)^2} + 676 \times 25 = 625 \times {(BD)^2} + 625 \times 2116\]
$676{(BD)^2} - 625{(BD)^2} = 625 \times 2116 - 676 \times 25$
$(672 - 625){(BD)^2} = 25(25 \times 2116 - 676)$
$51{(BD)^2} = 25 \times 4(25 \times 529 - 169)$
$51{(BD)^2} = 100(13225 - 169)$
$51{(BD)^2} = 100(13056)$
${(BD)^2} = \dfrac{{100 \times 13056}}{{51}}$
${(BD)^2} = 100 \times 256$ …..(ii)
$256 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2$
$256 = {(2 \times 2 \times 2 \times 2)^2}$
$256 = {(16)^2}$
Now, we will substitute the value of $256$ in equation (ii) , we have
So, ${(BD)^2} = 100 \times {(16)^2}$
${(BD)^2} = {(10)^2} \times {(16)^2}$
${(BD)^2} = {(10 \times 16)^2}$
So, $BD = \sqrt {{{(10 \times 16)}^2}} $
$BD = 160$meters
Hence, the required answer is 160 meters.

Note: Students must know that an angle bisector divides the angle into two angles with equal measures. We will find the value of BD with the help of Pythagoras theorem.