Question

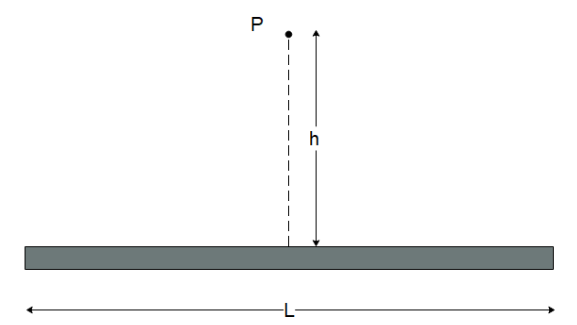
A total charge $ Q $ is distributed uniformly along a straight rod of Length $ L $ . The potential at a point P at a distance $ h $ from the midpoint of the rod is

(Hint: $ \;\int {\dfrac{1}{{\sqrt {{x^2} + {a^2}} }}dx = \ln \left( {x + \sqrt {{x^2} + {a^2}} } \right)} $
A) $ \dfrac{Q}{{4\pi {\varepsilon _0}L}}\ln \left( {L + \sqrt {{L^2} + 3{h^2}} } \right) $
B) $ \dfrac{Q}{{4\pi {\varepsilon _0}L}}\ln \left( {\dfrac{{L + \sqrt {{L^2} + 4{h^2}} }}{2}} \right) $
C) $ \dfrac{Q}{{4\pi {\varepsilon _0}L}}\ln \left( {\dfrac{{L + \sqrt {{L^2} + 4{h^2}} }}{{L - \sqrt {{L^2} + 4{h^2}} }}} \right) $
D) $ \dfrac{Q}{{4\pi \varepsilon {{_{}^{}}_0}L}}\ln \left( {\dfrac{{\sqrt {{L^2} + 4{h^2}} + L}}{{\sqrt {{L^2} + 4{h^2}} - L}}} \right) $

Answer 1

Hint: In this solution, we will calculate the potential due to a charge due to a small charge element of the rod at the point P. Then we will integrate the potential due to the small element over the limits of the length of the rod.

Complete step by step answer:
In the situation given to us, let us take a small element of the rod and calculate the potential due to it on the point P.

We can see that the potential due to the charge element at point P will be calculated as:
 $ dV = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{dq}}{r} $ where $ dq $ is the charge element and $ r $ is the distance of the charge element from the point P.
The distance $ r $ can be determined from Pythagoras’s theorem as
 $ r = \sqrt {{h^2} + {x^2}} $
Now the charge contained by the charge element $ dq $ can also be determined as $ dq = \dfrac{Q}{L}dx $ (as the rod has uniform charge density)
So, the potential due to the charge element will be simplified as
 $ dV = \dfrac{Q}{{4\pi {\varepsilon _0}L}}\dfrac{{dx}}{{\sqrt {{h^2} + {x^2}} }} $
The net potential due to the entire rod can be calculated by integrating the potential due to the charge element from the limits of the rod which are $ x = - L/2 $ and $ x = L/2 $ as
 $ V = \dfrac{Q}{{4\pi {\varepsilon _0}L}}\int\limits_{x = - L/2}^{x = L/2} {\dfrac{{dx}}{{\sqrt {{h^2} + {x^2}} }}} $
We know that $ \;\int {\dfrac{1}{{\sqrt {{x^2} + {a^2}} }}dx = \ln \left( {x + \sqrt {{x^2} + {a^2}} } \right)} $ so taking $ a = h $ , we can write
 $ V = \dfrac{Q}{{4\pi {\varepsilon _0}L}}\;\left. {\ln \left( {x + \sqrt {{x^2} + {a^2}} } \right)} \right|_{x = - L/2}^{x = L/2} $
On placing the limits of integration, we get
 $ V = \dfrac{Q}{{4\pi {\varepsilon _0}L}}\ln \left( {\dfrac{{\sqrt {{L^2} + 4{h^2}} + L}}{{\sqrt {{L^2} + 4{h^2}} - L}}} \right) $
Hence the correct choice is option (D).

Note:
We need to integrate the potential as the distance of all the charge elements will be different from the point of interest. While placing the limits, we should be careful to place the limits from $ x = - L/2 $ and $ x = L/2 $ and not $ x = 0 $ to $ x = L $ as we are calculating the potential from the midpoint of the rod and we’ve set the geometry of the problem accordingly.