Question

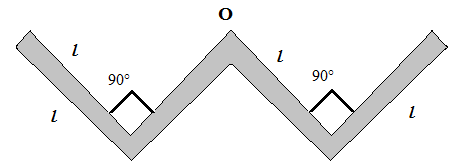
A thin uniform rod of length 4l, mass 4m is bent at the points as shown in the fig. What is the moment of inertia of the rod about the axis passing point O and perpendicular to the plane of the paper?

A. $\dfrac{ml^2}{3}$
B. $\dfrac{10ml^2}{3}$
C. $\dfrac{ml^2}{12}$
D. $\dfrac{ml^2}{24}$

Answer 1

Hint: This question can merely be solved by using parallel axis theorem and use of some simple geometry. Though the question might appear complicated, we still have some symmetry. We can break the rod from the middle and get two equal V.

Formula used:
Parallel axis theorem:
The moment of inertia of a body about an axis parallel to its centre of mass axis is given by:
$I = I_{CM} + Md^2$
where l is the length from the centre to the required axis.

Complete answer:
Break the W from the middle first, as we can get the result as twice of this.
Now, we have 2 further segments. Let's treat them one by one.
Consider the one attached to the axis in question:
Its centre has a distance of (l/2) from the axis so on applying parallel axis theorem, we get:
$I_1 = \dfrac{Ml^2}{12} + \dfrac{Ml^2}{4}$
$I_1 = \dfrac{Ml^2}{3}$
Where we know that a rod of length L has a moment of inertia of
$\dfrac{ML^2}{12}$
perpendicular to the length through the centre.

Now, for the remaining length (of our V), we observe a right angled triangle forming as:

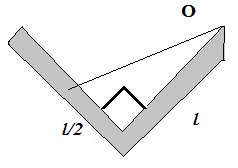
So, the distance from the axis to the centre of this segment becomes:
$d = \sqrt{\dfrac{l^2}{4} + l^2}$
$d = \sqrt{\dfrac{5l^2}{4}}$
Keeping this in the parallel axis theorem:
$I_2 = \dfrac{Ml^2}{12} + \dfrac{5Ml^2}{4}$

$I_2 = \dfrac{4 Ml^2}{3}$
Adding the two contributions we get:

$I_1+ I_2 = \dfrac{5 Ml^2}{3}$

This is for only half of our W. For the other half, we just make twice of this so we get,
$2(I_1+ I_2 )= \dfrac{10 Ml^2}{3}$

So, the correct answer is “Option D”.

Note:
In the moment of inertia questions, always the axis should be noted correctly. If we misplace the axis, the entire solution changes. Like in our case, we measured the distances of the centre of both rod segments from the point O which was given to us as perpendicular to the plane of paper (from O).