Question

A thin semicircular conducting ring (PQR) of radius r is falling with its plane vertical in a horizontal magnetic field B, as shown in Fig. The potential difference developed across the ring when its speed is \[v\],

A). \[Zero\]
B). \[\dfrac{\text{Bv }\!\!\pi\!\!\text{ }{{\text{r}}^{\text{2}}}}{\text{2}}\text{and P is at higher potential}\]
C). \[\text{ }\!\!\pi\!\!\text{ rBv and R is at higher potential}\]
D). \[\text{2rBv and R is at higher potential}\]

Answer 1

Hint: Here the circular coil is falling vertical to the magnetic field. We know that when a conductor moves in a magnetic field an emf will be induced. This principle is known as Faraday’s law of electromagnetic induction. This induced emf depends on the velocity and length of the conductor and the magnetic field. We can find out the potential difference using the equation for induced emf and the point at a higher potential.

Formula used:
\[e=l\left( v\times B \right)\]
\[v\times B=vB\sin \theta \]

Complete step-by-step solution:

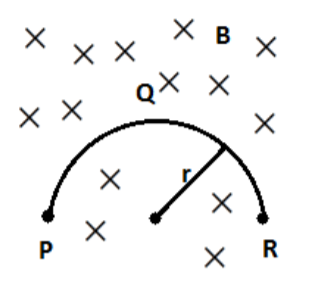
From the figure, we can understand that the magnetic field is directed into the plane of paper. Whenever a current-carrying conductor moves in a magnetic field, an emf will be induced, which is given by, Induced emf, \[e=l\left( v\times B \right)\]
Where,
\[v\] is the velocity of the conductor
\[B\] is the magnetic field
\[l\] is the length of the conductor
As the conductor is falling vertically, the velocity of the conductor will be perpendicular to the magnetic field.
Then,
\[\left( v\times B \right)=vB\sin 90=vB\]
Then,
\[e=BVl\] ------ 1
Given that the radius semicircle is \[r\]. Then its diameter is \[2r\] which is equal to
the length \[l\].
\[l=2r\]
Then,
\[e=2rBV\]
Hence, magnetic force acting will be perpendicular to both \[\text{v and B}\].

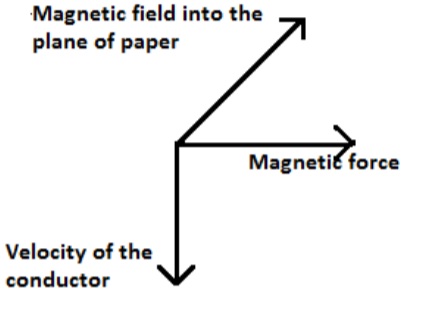
Then, the direction of induced emf will be from R to P. We know that emf flows from higher potential to lower potential. Hence, R is at a higher potential.

Therefore, the potential difference developed across the ring is \[E=2rBV\] and R is at the higher potential. Hence the answer is option D.

Note: To determine the directions, right hand rule can be used. It shows that the magnetic field, force, and velocity of the conductor are perpendicular to each other. If we are using the equation \[e=BVl\], then \[B\], \[V\] and \[l\] are considered to be perpendicular to each other. If anyone of these, \[\vec{v}\parallel \vec{B}\], \[l\parallel \vec{B}\] and \[\vec{v}\parallel l\] conditions satisfy, then the induced emf in the circuit is zero.