Question

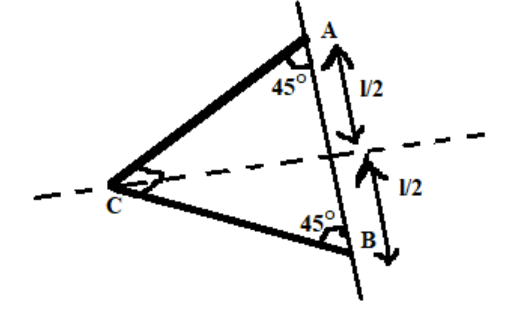
A thin rod of Linear mass density \[\lambda \] at right angle at its mid point (C) and fixed to points A and B such that it can rotate about an axis passing through AB. The moment of inertia about an axis passing through AB is:-

(A) \[\dfrac{{\lambda {l^3}}}{{6\sqrt 2 }}\]
(B) \[\dfrac{{\lambda {l^3}}}{{2\sqrt 2 }}\]
(C) \[\dfrac{{\lambda {l^3}}}{4}\]
(D) \[\dfrac{{\lambda {l^3}}}{{\sqrt 2 }}\]

Answer 1

Hint: In this, we will consider the small part of the rod first. Then calculate the moment of inertia for the small part then we will integrate the small moment of inertia for finding the net moment of inertia for both the rod. As we know the formula for the moment of inertia \[\left( {I = m{r^2}} \right)\]. By using this we can simplify this question.

Complete step by step answer:
Length of the rod is =\[\dfrac{1}{{\sqrt 2 }}\]
Linear density of rod is= \[\lambda \]
Let a small part \[dx\] be at a distance x from the first rod.
So, small mass (\[dm\])=\[\lambda dx\]
 Distance from axis \[x{\text{ }}cos{\text{ }}{45^\circ } = \dfrac{x}{{\sqrt 2 }}\]

Moment of inertia of \[dm\]about the axis is= \[dI = {\text{ }}dm\;{\left( {\dfrac{x}{{\sqrt 2 }}} \right)^{2\:}}\;\;\; = \dfrac{{\lambda {x^2}dx}}{2}\]
 Now, integrate this equation for calculate the value of I,
\[I = \int\limits_0^{\dfrac{l}{{\sqrt 2 }}} {\dfrac{{\lambda {x^2}dx}}{2}} \]
\[I = \dfrac{{\lambda {l^3}}}{{3 \times 4\sqrt 2 }}\]

Now, the second rod will also have the same moment of inertia. So, the net magnetic moment will be 2I, which is equal to=\[2\dfrac{{\lambda {l^3}}}{{3 \times 4\sqrt 2 }} = \dfrac{{\lambda {l^3}}}{{6\sqrt 2 }}\]

So, the correct answer is “Option A”.

Note:
Moment of inertia of a rigid body is the quantity that tells us about the torque which is needed for angular acceleration about the rotational axis. In simple words, we can say that the quantity which describes how easily a body can move about a given axis.
\[I = m{r^2}\]