Question

A thin conducting ring of radius R is given a charge +Q. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on the part ACDB of the ring is

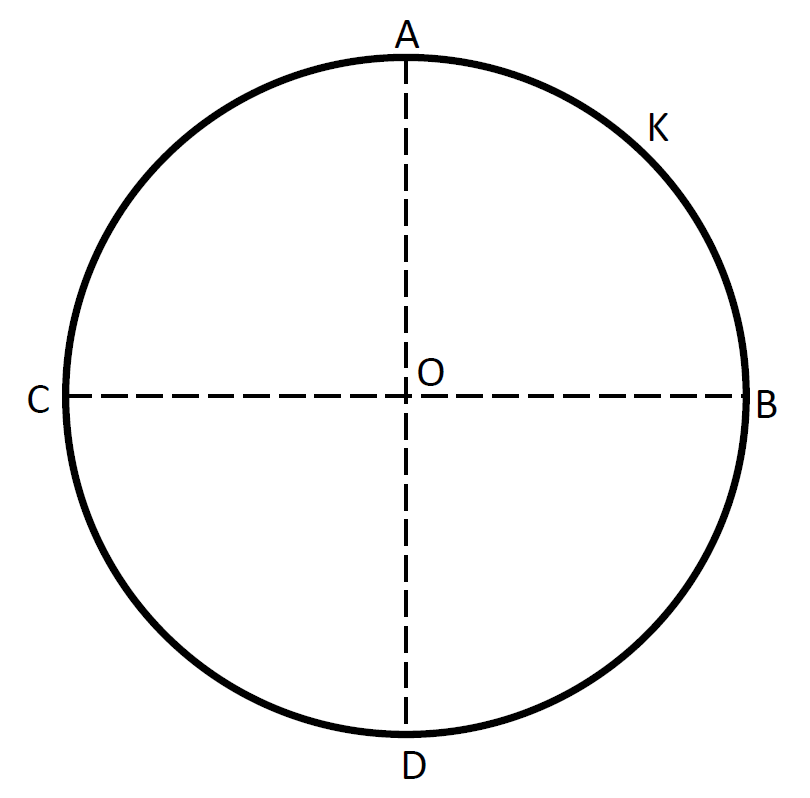
A. E along KO
B. 3E along OK
C. 3E along KO
D. E along OK

Answer 1

- Hint: Electric field is force per unit charge. Since it is a circular wire with constant radius the net force at the centre of the circle is zero due to the charge distributed on the ring. Therefore, the electric field due to arc AKB balances the electric field due to the remaining arc ACDB of the ring. Thus, the electric field is the same but in the opposite direction.

Complete answer:
Electric field at a point is force per unit charge. Now in the given problem, we have a conducting wire shaped as a circle with constant radius R. It has been given a charge Q. Since the wire is conducting the charge will be distributed uniformly throughout the wire. As soon as the wire is charged, there will be an electric field developed at all points in space around the wire.
Consider the center of the circle O. It is equidistant from all the points on the wire. We have been provided with one information that the electric field due to the arc AKB at the center is E. Since the center is equidistant from the wire the net force at the point due to charge distributed throughout the wire remains zero. We are asked to find the magnitude of the electric field due to the arc ACDB, which is the rest of the circular wire.
We have been given that the charge distributed in wire as positive and thus the electric field, E, at O due to arc AKB is directed from K to O. To balance this field arc ACDB will exert equal electric field, E, at O in the opposite direction that is from O to K. So, option D is the correct answer to the question. The following diagram shows the opposing electric field lines at center O.

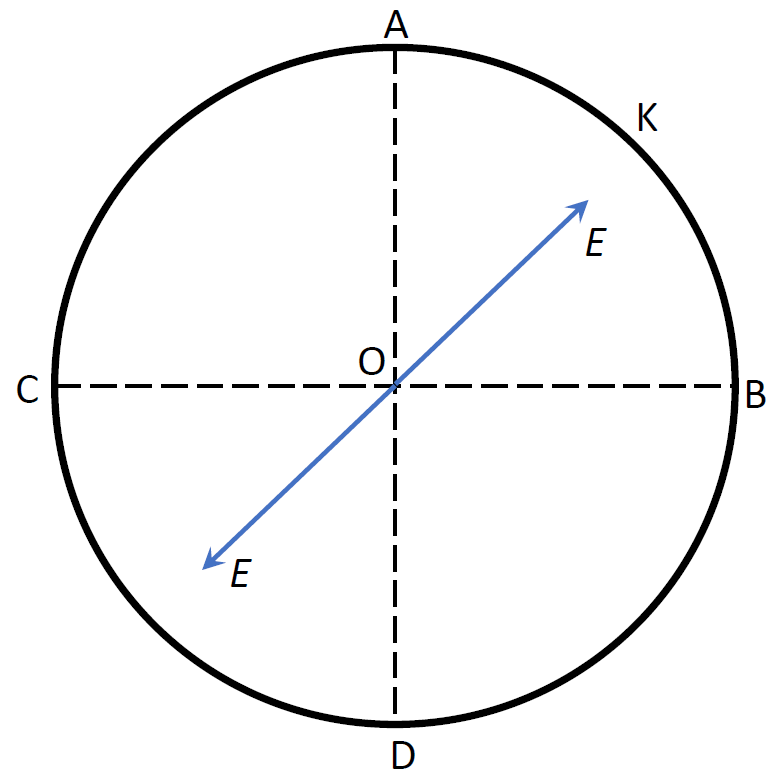
Note: Above method is short without any mathematical expression and uses the definition of electric field and balance of forces. But you can come to the same solution if you consider small elements of the circular ring and try to find an expression of electric at the centre due to these elemental charges and find the direction of the resultant electric field due to arcs AKB and ACDB.