Question

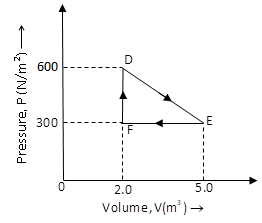
A thermodynamic system is taken from an original state to an intermediate state by the linear process shown in the figure. Its volume is then reduced to the original value from \[E\]to \[F\]by an isobaric process. Calculate the total work done by the gas from \[D\] to\[E\] to $F$.

A $225J$
B $450J$
C $900J$
D $600\,J$

Answer 1

Hint: The area under the pressure-volume curve is numerically equal to the work done by a system or on the system. Determine the area which lies under the given processes in the thermodynamic process. Calculate the area under the curve using the pressure and volume scales given in the graph to determine the total work done by the gas.

Complete step by step answer:
We have given the pressure-volume curve of a thermodynamic process. It is also given that the volume of the gas is reduced from E to F by an isobaric process which means that while the volume of the gas is decreasing, the pressure of the gas is constant.

We have to determine the total work done by the gas from D to E to F.

The total work done $W$ by the gas from D to E to F is the sum of the work done ${W_{DE}}$ by the gas form D to E and the work done ${W_{EF}}$ by the gas from E to F.
$W = {W_{DE}} + {W_{EF}}$

The work done by a thermodynamic system in an isobaric process is equal to the area under the pressure-volume curve for that thermodynamic process.

Hence, the work done by the gas form D to E to F is equal to the area of the triangle DEF.

The area of triangle DEF is given by
$Area\,of\,\,triangle\,\,DEF = \dfrac{1}{2}\left( {DF \times FE} \right)$ …… (1)

The value of the side DF of triangle DEF is the change in the pressure ${P_F}$ of the gas at F and pressure ${P_D}$ at D.
$ \Rightarrow DF = {P_F} - {P_D}$

Substitute \[600\,{\text{N/}}{{\text{m}}^2}\] for ${P_F}$ and \[300\,{\text{N/}}{{\text{m}}^2}\] for ${P_D}$ in the above equation.
\[ \Rightarrow DF = \left( {600\,{\text{N/}}{{\text{m}}^2}} \right) - \left( {300\,{\text{N/}}{{\text{m}}^2}} \right)\]
\[ \Rightarrow DF = 300\,{\text{N/}}{{\text{m}}^2}\]

The value of the side FE of triangle DEF is the change in the volume ${V_E}$ of the gas at E and volume ${V_F}$ at E.
$ \Rightarrow DF = {V_E} - {V_F}$

Substitute \[5.0\,{{\text{m}}^3}\] for ${V_E}$ and \[2.0\,{{\text{m}}^3}\] for ${V_F}$ in the above equation.
\[ \Rightarrow FE = \left( {5.0\,{{\text{m}}^3}} \right) - \left( {2.0\,{{\text{m}}^3}} \right)\]
\[ \Rightarrow FE = 3.0\,{{\text{m}}^3}\]

Substitute \[300\,{\text{N/}}{{\text{m}}^2}\] for $DF$ and \[3.0\,{{\text{m}}^3}\] for $FE$ in equation (1).
$Area\,of\,\,triangle\,\,DEF = \dfrac{1}{2}\left[ {\left( {300\,{\text{N/}}{{\text{m}}^2}} \right) \times \left( {3.0\,{{\text{m}}^3}} \right)} \right]$
$Area\,of\,\,triangle\,\,DEF = 450\,{\text{J}}$

Therefore, the area under the curve and hence, the work done by the gas is $450\,{\text{J}}$.

Hence, the correct option is B.

Note:
The students should correctly determine the area under the curve to determine the total work done by the gas. One can also determine the total area under the curve by taking the sum of the area under all the individual processes shown in the given pressure-volume graph. But the signs of the work done should be taken properly while determining the total final work done by the gas.