Question

(a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or atmosphere?
(b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet's velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?
(c) An artificial satellite orbiting the Earth in a very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to Earth?
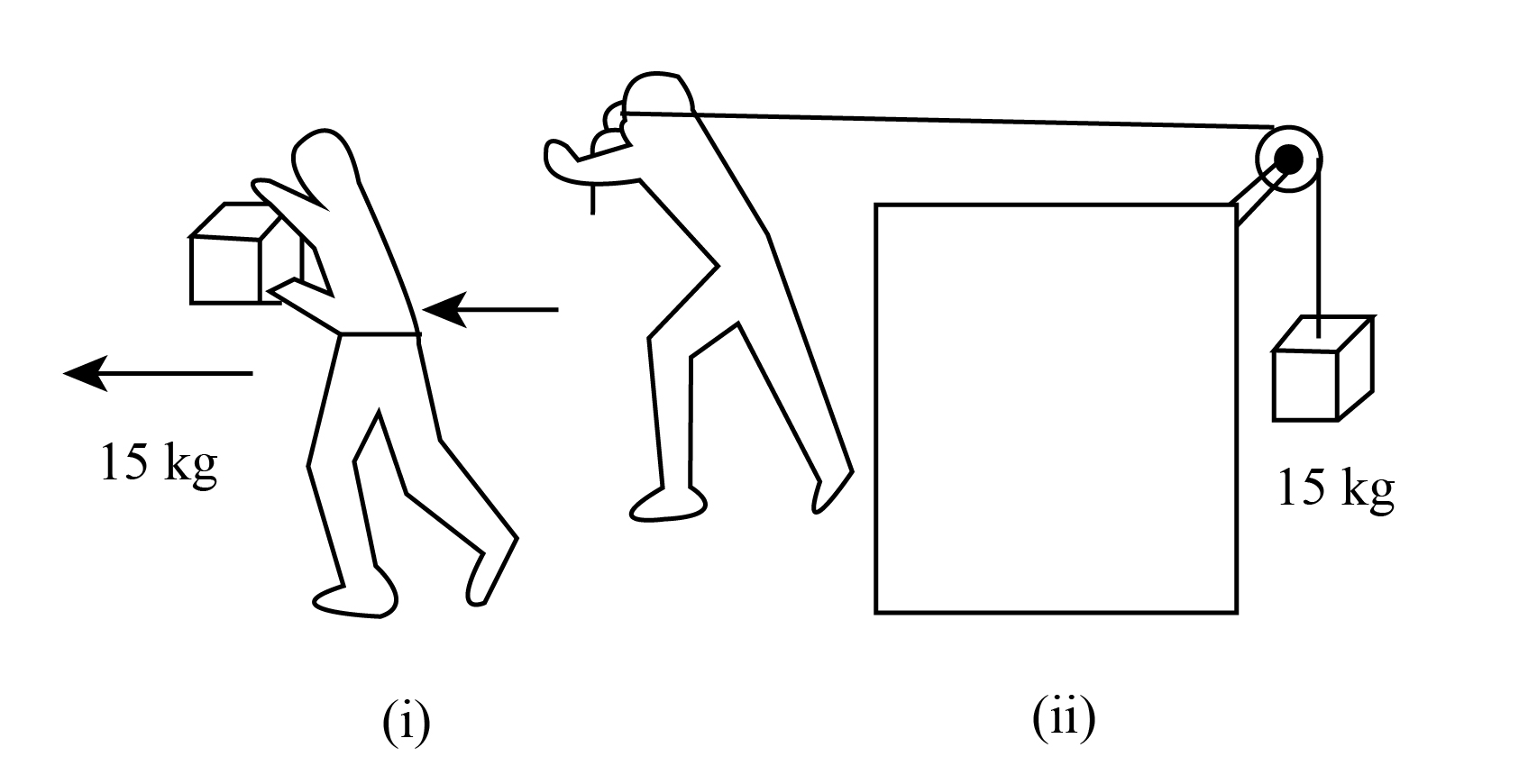
(d) In Fig. (i) the man walks 2m carrying a mass of 15 kg on his hands. In Fig (ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley and a mass of 15 kg hangs at its other end. In which case is the work done greater?

Answer 1

Hint: We know that friction generates heat and the work done against friction is manifested by the generation of heat and depicted as loss of work. The work done by a conservative force on a conservative field is always zero. Hence we can say that the total energy of the satellite remains constant in absence of dissipative forces. We also know that the amount of the work done depends on the angle between force and displacement that is $\theta $.

Complete step by step solution:
The rocket itself generates heat that is required for the burning of the casing. The work done against the frictional force reappears as heating of the casing of the rocket as the kinetic energy of the rocket continuously decreases.
Work done by the conservative force over the closed path is zero and it does not matter how the shape of the closed path is, and hence work done is zero as the angle between force and displacement is zero.
Since the total energy of the satellite, E is constant and it is the sum of gravitational potential energy GPE and kinetic energy KE. As the satellite enters into the atmospheric region its GPE decreases and to make the total energy E constant, its KE increases.
In fig(i), since the man is carrying a block in his hands, hence the angle between the displacement and weight of the block is perpendicular. Therefore, $\theta $ is equal to 900. Hence the work done becomes,
\[ \Rightarrow W = F \times s\cos 90^\circ \]
\[ \Rightarrow W = 0\]
In fig(ii) since the man is pulling the rope and hence he is applying force in the horizontal direction. Therefore, the angle between force and displacement is $\theta = 90^\circ $. Therefore,
$ \Rightarrow W = F \times s\cos 0^\circ $
\[ \Rightarrow W = mg \cdot s\]
\[ \Rightarrow W = 15 \times 9.8 \times 2\]
\[\therefore W = 294\;J\]

Note:
The total energy of the body remains constant always. The potential energy and kinetic energy keep on converting to each other. Whereas in the case of dissipative forces the potential energy decreases and kinetic energy changes accordingly.