Question

A tank that opens at the top is made of iron sheet 4 m wide. If the dimensions of the tank are \[12m\times 8m\times 6m\], find the cost of the iron sheet used at the rate of Rs. 17.50 per meter.

Answer 1

Hint: Assume that the required length of the iron sheet is \[x\] meters. The width of the iron sheet is 4 meters. Now, use the formula, Area = Length \[\times \] Width, and calculate the area of the iron sheet. The length, width, and height of the tank are 12 meters, 8 meters, and 6 meters respectively. Use the formula for the area of four walls, Area of four walls = 2(Width \[\times \] Height + Length \[\times \] Height). Similarly, use the formula, Area = Length \[\times \] Width, and calculate the area of the base of the tank. Calculate the total area of the tank by adding the area of the base and area of four walls. Since the iron sheet is used along the area of the tank, so the area of the sheet must be equal to the area of the walls of the tank. Solve it further and get the value of x. Use the information that the cost of the iron sheet is used at the rate of Rs. 17.50 per meter and calculate the cost.

Complete step-by-step solution
According to the question, we are given that a tank that opens at the top is made of iron 4 m wide. The dimension of the tank is \[12m\times 8m\times 6m\].
Now, we have
The length of the tank = 12 m …………………………………….(1)
The width of the tank = 8 m …………………………………….(2)
The height of the tank = 6 m …………………………………….(3)
The width of the iron sheet = 4 m ……………………………………………(4)
The tank is open at the top so our tank will look like,

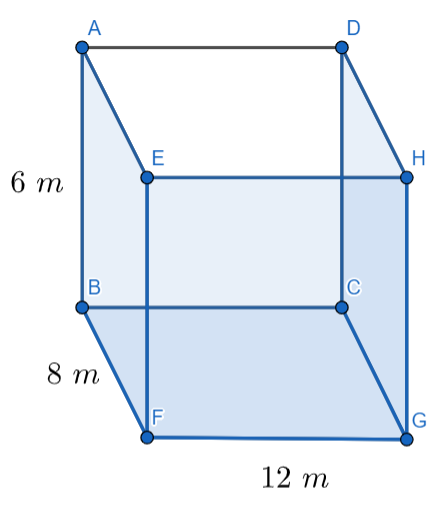
First of all, let us assume that the required length of the iron sheet is \[x\] meters ………………………………..(5)

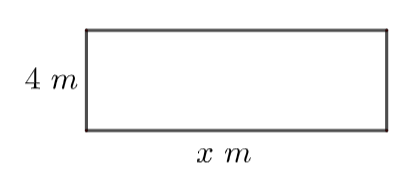
We know the formula for the area of the rectangle, Area = Length \[\times \] Width …………………………………(6)
Now, from equation (4), equation (5), and equation (6), we get
The area of the iron sheet = \[x\times 4\,{{m}^{2}}=4x\,{{m}^{2}}\] ……………………………………………(7)
We know the formula for the area of four walls, Area of four walls = 2(Width \[\times \] Height + Length \[\times \] Height) ………………………………………….(8)
Now, using the formula shown in equation (8), we get
The area of four walls of the tank = \[2\left( 8\times 6+12\times 6 \right)\,{{m}^{2}}=2\left( 48+72 \right)\,{{m}^{2}}=240\,{{m}^{2}}\] ………………………………………………………..(9)
Here, we also have to include the area of the base.
Using the formula shown in equation (6), we get
The area of the base of the tank, BCGF = Length \[\times \] Width = 12m \[\times \] 8 m = 96 \[{{m}^{2}}\] …………………………………………….(10)
From the figure, we can say that the total area of the tank is the summation of the area of four walls of the tank and the area of the base of the tank, BCGF. So,
The total area of the tank = The area of four walls of the tank + The area of the base of the tank, BCGF ……………………………………………………….(11)
On adding equation (9) and equation (10), we get
The total area of the tank = 240 \[{{m}^{2}}\] + 96 \[{{m}^{2}}\] = 336 \[{{m}^{2}}\] ………………………………………(12)
Since the iron sheet is used along the area of the tank so, the area of the sheet must be equal to the area of the walls of the tank ………………………………………………(13)
From equation (7), equation (12), and equation (13), we get
\[\begin{align}
  & \Rightarrow 4x=336 \\
 & \Rightarrow x=\dfrac{336}{4} \\
 & \Rightarrow x=84 \\
\end{align}\]
So, the required length of the iron sheet is 84 meters ………………………………….(14)
We are also given that the cost of the iron sheet is Rs. 17.50 per meter …………………………………(15)
Now, from equation (14) and equation (15), we get
The cost of iron sheet = Rs. \[84\times 17.5\] = Rs. 1470.
Therefore, the cost of the iron sheet is Rs. 1470.

Note: For this question, where we require the area of four walls. The formula for the area of four walls, Area of four walls = 2(Width \[\times \] Height + Length \[\times \] Height). Also, here one might include the area of the top of the tank while calculating the total area of the tank. Since the tank is open at the top, we have to ignore the area of the top of the tank.