Question

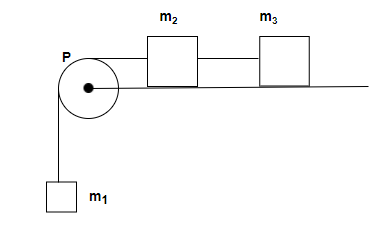
A system consists of three identical masses m₁​, m₂​ and m₃​ connected by a string passing over a pulley P. The mass m₁​ hangs freely and m₂​ and m₃​ are on a rough horizontal table (the coefficient of friction \[ = \mu \]). The pulley is frictionless and of negligible mass. The downward acceleration of mass m₁​ is:

Answer 1

Hint: This given problem can be solved by taking the consideration of motion of bodies on a frictional surface and under the gravitational force when these bodies are connected with each other by a string and hanged on some light and frictionless pulley.

Step-by-step solution:
Step 1: As given in the question three identical masses \[\mathop m\nolimits_1 \]​, \[\mathop m\nolimits_2 \]​ and \[\mathop m\nolimits_3 \]​ connected by a string passing over a pulley P. The mass \[\mathop m\nolimits_1 \]​ is hanging freely and other two masses \[\mathop m\nolimits_2 \]​ and \[\mathop m\nolimits_3 \] are kept at the surface and the frictional coefficient of this surface is \[\mu \].

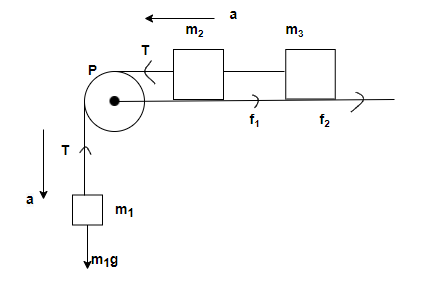
Let us consider that the mass \[\mathop m\nolimits_1 \] moves downward with acceleration \[a\]. So, the masses \[\mathop m\nolimits_2 \]​and \[\mathop m\nolimits_3 \]also move on horizontal surface with acceleration \[a\].
The given pulley is light in weight and frictionless so tension \[T\] in the string will be the same at each n every point.
As shown in the above figure forces should be balanced out for the closed system.
Step 2: So, for the motion of horizontal blocks –
\[\left( {\mathop m\nolimits_2 + \mathop m\nolimits_3 } \right)a = T - \mathop f\nolimits_1 - \mathop f\nolimits_2 \]; where \[\mathop f\nolimits_1 \] is frictional force on mass \[\mathop m\nolimits_2 \], \[\mathop f\nolimits_2 \] is frictional force on mass \[\mathop m\nolimits_3 \], and \[\left( {\mathop m\nolimits_2 + \mathop m\nolimits_3 } \right)a\] is force on masses \[\mathop m\nolimits_2 \]​and \[\mathop m\nolimits_3 \] due to acceleration.
It is given that all three masses are identical so let \[\mathop m\nolimits_{1 = } \mathop m\nolimits_{2 = } \mathop m\nolimits_3 = m\]
And, \[\mathop f\nolimits_1 = \mathop f\nolimits_2 = \mu mg\] i.e. frictional forces on masses \[\mathop m\nolimits_2 \]​and \[\mathop m\nolimits_3 \].
\[2ma = T - 2\mu mg\] …………………..(1)
Step 3: For the motion of vertical block –
\[\mathop m\nolimits_1 a = \mathop m\nolimits_1 g - T\] or
\[ma = mg - T\] ……………………………..(2)
So, from equation (1) and (2), we will get
\[T = mg - ma\]
\[2ma = mg - ma - 2\mu mg\] on rearranging this equation, we will get –
\[3ma = \left( {1 - 2\mu } \right)mg\]on further solving this equation
\[a = \dfrac{{\left( {1 - 2\mu } \right)g}}{3}\]

So, the correct answer is \[a = \dfrac{{\left( {1 - 2\mu } \right)g}}{3}\].

Note:
-It should be remembered that friction always opposes the relative motion and because of that frictional force will always be opposite to the motion due to acceleration.
-Remember that friction will be there only when the body is actually sliding/rolling over the surface of another body.