Question

A student sitting in a classroom sees a picture on the black board at a height of 1.5m from the horizontal level of sight. The angle of elevation of the picture is \[{{30}^{\circ }}\] . As the picture is not clear to him, he moves straight towards the black board and sees the picture at an angle of elevation of \[{{45}^{\circ }}\] . Find the distance by which the student moves.
 A. 1.098m
B. 2.098m
C. 3.098m
D. None of these

Answer 1

Hint: Here, for answering this question we will first visualize the situation and draw a diagram and later, we will assume the distance not given in the question as x and y and using the tangent formula as we know the angles of elevation we will find their values.
We know that the formula for tangent of an angle is
\[\tan \theta =\dfrac{Perpendicular}{\text{Base}}\] .

Complete step by step answer:
From the information given in the question, the figure we visualize would look like the below picture.

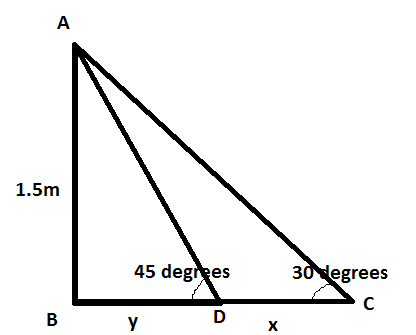
By inspecting the figure, we have
 The height of the picture on the black board AB =1.5 m (given in the question).
From the question we know that, the angles of elevation for the top of the picture are \[{{30}^{\circ }}\] and \[{{45}^{\circ }}\] from different positions D and C.
 Let us assume that the distance between C and D be x m and the distance between D and B be y m.
Using the formula for tangent in the \[\Delta ACB\] , we get
\[\begin{align}
  & \tan {{30}^{\circ }}=\dfrac{1.5}{x+y} \\
 &\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{1.5}{x+y} \\
 &\Rightarrow x+y=\left( 1.5 \right)\sqrt{3}\ \ \ \ \ ...(a) \\
\end{align}\]
Similarly, using the formula for tangent in the \[\Delta BDA\] , we get
\[\begin{align}
  & \tan {{45}^{\circ }}=\dfrac{1.5}{y} \\
 &\Rightarrow 1=\dfrac{1.5}{y} \\
 &\Rightarrow y=1.5\ m \\
\end{align}\]
Now, using the value of y, we will get
\[\begin{align}
  & x=\left( 1.5 \right)\sqrt{3}-y \\
 &\Rightarrow x=\left( 1.5 \right)\sqrt{3}-1.5 \\
 &\Rightarrow x=1.5\left( \sqrt{3}-1 \right)\ m \\
\end{align}\]

Hence, the student moves by a distance of \[1.5\left( \sqrt{3}-1 \right)\ m=1.098m\] .

Note: In questions of this type, the importance of the figure is very high and without the figure we could not do this type of question, because by drawing a figure we will be more clear with the content of the question. If not, we can make an error while drawing the figure and then end up making a mistake and we would conclude with a completely wrong solution.