Question

A student is experimenting with a resonance tube apparatus in a Physics lab to find the speed of sound at room temperature. He got resonating lengths of air columns as $17cm$ and $51cm$, using tuning forks of frequency $512Hz$. Find speed of sound at the room temperature and specify, whether the side water reservoir was moved upward or downward to obtain the second resonance ($51cm$)?
A. $348{\text{ }}m/s$, downwards
B. $348{\text{ }}m/s$, upwards
C. $332{\text{ }}m/s$, downwards
D. $332{\text{ }}m/s$, upwards

Answer 1

Hint: The resonance tube is considered to be an open organ pipe. So, for first resonance, there is one node and one antinode, whose length is a quarter of the wavelength of the sound wave. The water inside the reservoir will move upward, as the resonances increase, successively.

Formula used:
${f_1} = \dfrac{{{v_s}}}{{4{L_1}}}$

Complete answer:
First let us draw a rough diagram of resonance tube apparatus. It is mentioned in the problem that the student got resonating columns at $17cm$ and $51cm$. This indicates that at $17cm$ the first resonance occurs and at $51cm$ the second resonance occurs.

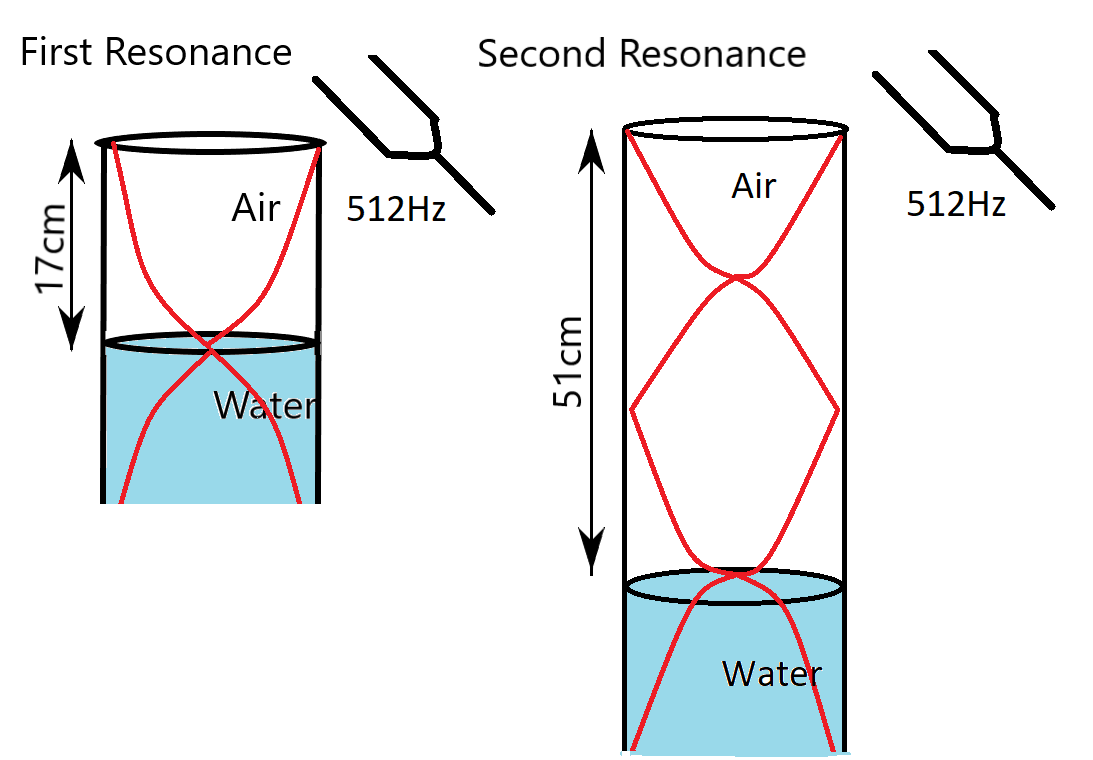
The condition for first resonance is
${f_1} = \dfrac{{{v_s}}}{{4{L_1}}}$
Where
${f_1}$ is the first resonance frequency
${v_s}$ is the velocity of the sound
${L_1}$ is the length at which first resonance occurs
We have ${f_1} = {\text{ }}512Hz$ and ${L_1} = {\text{ }}17cm$. Substituting this in the first resonance condition
$\eqalign{
  & {f_1} = \dfrac{{{v_s}}}{{4{L_1}}} \Rightarrow {v_s} = {f_1} \times 4{L_1} \cr
  & \Rightarrow {v_s} = 512 \times 4\left( {17 \times 1{0^{ - 2}}} \right) = 348.16m{s^{ - 1}} \cr
  & \therefore {v_s} = 348.16m{s^{ - 1}} \sim 348m{s^{ - 1}} \cr} $
Now, for the second part of the answer, we have actually increased the air column compared to the first resonance. So, the water level would have reduced, in the resonance tube. This will compensate as an increase of water level in the side water reservoir. This shows as an upward movement of water in the side water reservoir.

So, the correct answer is “Option B”.

Note:
The above problem can also be solved using the condition for second resonance i.e.,
${f_2} = \dfrac{{3{v_s}}}{{4{L_2}}}$
Where
${f_2}$ is the second resonance frequency
${v_s}$ is the velocity of the sound
${L_2}$ is the length at which second resonance occurs.
Substituting the values given, we have
$\eqalign{
  & {f_2} = \dfrac{{3{v_s}}}{{4{L_2}}} \cr
  & \Rightarrow {v_s} = {f_2} \times \dfrac{{4{L_2}}}{3} \cr
 & \Rightarrow {v_s} = 512Hz \times \dfrac{{4 \times \left( {51 \times {{10}^{ - 2}}} \right)}}{3} =348.16m{s^{ - 1}} \cr
  & \therefore {v_s} = 348.16m{s^{ - 1}} \sim 348m{s^{ - 1}} \cr} $