Question

A straight tree breaks due to a storm and the broken part bends so that the top of the tree touches the ground making an angle of \[{{30}^{\circ }}\]with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 meters. The height of the tree is:
(a) \[10\left( \sqrt{3}+1 \right)m\]
(b) \[10\sqrt{3}m\]
(c) \[10\left( \sqrt{3}-1 \right)m\]
(d) \[\dfrac{10}{\sqrt{3}}m\]

Answer 1

Hint: In this question, let us first draw the diagram to get a clear picture of what we have to find. Then apply the tangent formula to get the height of the tree which isn’t bent then we can get the length of the part that is bent. Now, adding these two gives the height of the tree.

Complete step-by-step solution -
Let us first draw the diagram with the given conditions in the question

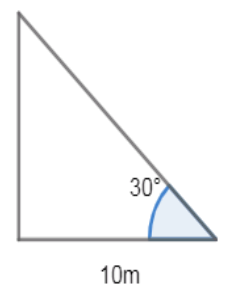
 Let us assume that the height of the tree which isn't bent as h and the length of the tree which is bent as x and the total height of the tree as H
Now, we can express H in terms of x and h as
\[\Rightarrow H=x+h\]
As we already know that tangent formula is given by
\[\tan \theta =\dfrac{\text{Opposite}}{\text{Adjacent}}\]
Now, let us apply this tangent formula to the above triangle
Here, we have opposite side as h and adjacent side as 10
Now, on substituting the respective values we get,
\[\Rightarrow \tan {{30}^{\circ }}=\dfrac{h}{10}\]
Now, this can be further written as
\[\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{h}{10}\]
Now, on rearranging the terms we get,
\[\therefore h=\dfrac{10}{\sqrt{3}}\]
Now, as the triangle is right angled triangle so we get,
\[\Rightarrow {{h}^{2}}+{{10}^{2}}={{x}^{2}}\]
Now, let us substitute the value of h in the above equation
\[\Rightarrow {{x}^{2}}={{\left( \dfrac{10}{\sqrt{3}} \right)}^{2}}+{{10}^{2}}\]
Now, on squaring the respective terms we get,
\[\Rightarrow {{x}^{2}}=\dfrac{100}{3}+100\]
Now, on further simplification we get,
\[\Rightarrow {{x}^{2}}=\dfrac{400}{3}\]
Let us now apply square root on both the sides
\[\Rightarrow x=\sqrt{\dfrac{400}{3}}\]
Now, on further simplification we get,
\[\therefore x=\dfrac{20}{\sqrt{3}}\]
Now, the height of the tree is given by
\[\Rightarrow H=x+h\]
Now, on substituting the respective values we get,
\[\Rightarrow H=\dfrac{20}{\sqrt{3}}+\dfrac{10}{\sqrt{3}}\]
Now, on simplifying further we get,
\[\Rightarrow H=\dfrac{30}{\sqrt{3}}\]
Now, on cancelling the common terms this can be further written as
\[\therefore H=10\sqrt{3}m\]
Hence, the correct option is (b).

Note: Instead of using the condition of the right-angled triangle to find the value of x we can also find it using the sine or cosine formula and then simplify further. Both methods give the same result.
It is important to note that we need to find the total height of the tree, not either bent length or the height of the tree that isn't bent. So, we need to add both the values to get the result.