Question

A straight line passes through the point $\left( {3,2} \right)$ and the portion of this line, intercepted between the positive axes, is bisected at this point. Find the equation of line?

Answer 1

Hint:Wherever we need the equation of a line we have to find only two things: point and a slope. The formula for the calculation of the slope of line is $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$. Bisection of a line means the division of a line into two equal halves. The line dividing it into two equal halves is called a bisector. We should know various forms of representing a straight line in order to find the equation of the required line.

Complete step by step answer:
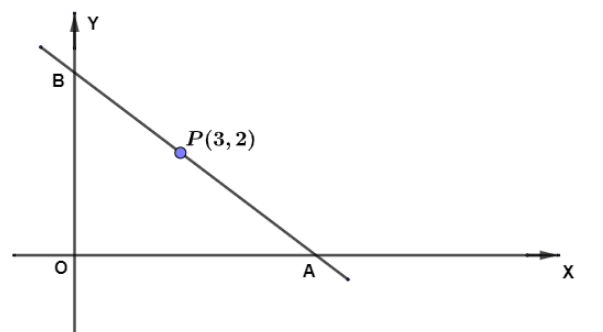
We know the two point form of a straight line as $\left( {y - {y_1}} \right) = \dfrac{{\left( {{y_2} - {y_1}} \right)}}{{\left( {{x_2} - {x_1}} \right)}}\left( {x - {x_1}} \right)$. So, we need to find the coordinates of two points lying on the required line.Let the line intersect the x axis and y axis at points $A\left( {a,0} \right)$ and $B\left( {0,b} \right)$ respectively. Let P be the point of bisection of the straight line intercepted between the axes.

Now, as we are given that the line is bisected at $\left( {3,2} \right)$. So, using the midpoint formula, we have the coordinates of midpoint of a line as \[\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)\]. So, we get the coordinates of the midpoint as \[\left( {\dfrac{{a + 0}}{2},\dfrac{{0 + b}}{2}} \right) = \left( {\dfrac{a}{2},\dfrac{b}{2}} \right)\].Hence, we get the coordinates of P as \[\left( {\dfrac{a}{2},\dfrac{b}{2}} \right)\]. Also, we are given the coordinates of point of bisection P as $\left( {3,2} \right)$.

So, equating both, we get,
\[ \Rightarrow \dfrac{a}{2} = 3\] and $\dfrac{b}{2} = 2$
So, finding the values of a and b by solving the equation using transposition method, we get,
\[ \Rightarrow a = 6\] and $b = 4$
Hence, the intercepts of the required line are $A\left( {6,0} \right)$ and $B\left( {0,4} \right)$.

Now, we have the coordinates of three points lying on the line given to us. So, we substitute the coordinates of two of these points into the two point form of a straight line.So, we get,
$\left( {y - 2} \right) = \dfrac{{\left( {0 - 2} \right)}}{{\left( {6 - 3} \right)}}\left( {x - 3} \right)$
$ \Rightarrow \left( {y - 2} \right) = \dfrac{{\left( { - 2} \right)}}{3}\left( {x - 3} \right)$
Cross multiplying the terms of the equation, we get,
$ \Rightarrow 3y - 6 = - 2x + 6$
Shifting all the constant terms to right side of the equation, we get,
$ \Rightarrow 3y + 2x = 6 + 6$
$ \therefore 3y + 2x = 12$

So, the equation of the required line passing through the point $\left( {3,2} \right)$ and bisected at the same point is $3y + 2x = 12$.

Note:We must know the two points form a straight line in order to find the equation of the required line. We also must know the formula for the midpoint of a line segment given the coordinates of the end point. One must have a good grip over concepts of coordinate geometry in order to tackle the problem.