Question

A straight highway leads to the foot of the tower. A man standing at the top of the tower observes a car at an angle of depression of \[{30^ \circ }\], which is approaching the foot of the tower with uniform speed. Six seconds later, the angle of depression of the car is found to be${60^ \circ }$. Find the time taken by the car to reach the foot of the tower from this point.

Answer 1

Hint:-In this question first we make a situation of questions with the help of applications of trigonometric angles. Then we find the relation among the time taken , height of tower, distance between points when an angle of depression changes from \[{30^ \circ }\]to ${60^ \circ }$.

Complete step-by-step answer:

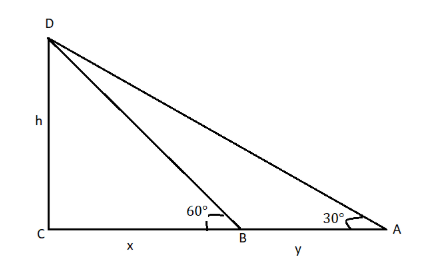
Let height of tower be h
$ \Rightarrow {\text{CD = h}}$
Angle of depression=${30^ \circ }$
After 6 seconds angle of depression changes to ${60^ \circ }$
So let distance covered in 6 sec be y and the distance of this point B from tower i.e. from C be x
$
   \Rightarrow {\text{AB = }}y \\
   \Rightarrow {\text{BC = }}x \\
 $
Now consider triangle BCD
$
   \Rightarrow \tan {60^ \circ } = \dfrac{{{\text{CD}}}}{{{\text{BC}}}} \\
   \Rightarrow \sqrt 3 = \dfrac{h}{x} \\
   \Rightarrow h = \sqrt 3 x{\text{ eq}}{\text{.1}} \\
$
Now consider triangle ACD
$
   \Rightarrow \tan {30^ \circ } = \dfrac{{{\text{CD}}}}{{{\text{AC}}}} \\
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{x + y}} \\
   \Rightarrow x + y = \sqrt 3 {\text{h eq}}{\text{.2}} \\
 $
From eq.1 we can rewrite eq.2
$
   \Rightarrow x + y = \sqrt 3 (\sqrt 3 )x \\
   \Rightarrow x + y = 3x \\
   \Rightarrow y = 2x{\text{ eq}}{\text{.3}} \\
 $
Now, it is given that a car moves from point A to point B in 6 sec.
Let speed =$k$kmps
Since, Time= $\dfrac{{{\text{Distance}}}}{{{\text{Speed}}}}$
Put time=6sec
Distance=y
Then
$
   \Rightarrow 6 = \dfrac{y}{k} \\
   \Rightarrow y = 6k{\text{ eq}}{\text{.4}} \\
 $
On putting value of y in eq.3, we get
$
   \Rightarrow 6k = 2x \\
   \Rightarrow x = 3k{\text{ eq}}{\text{.5}} \\
$
Now , the time taken to go from point B to tower is
${\text{time = }}\dfrac{{{\text{Distance}}}}{{{\text{Time}}}}$
$ \Rightarrow {\text{time = }}\dfrac{x}{k}$
Now, put value of x from eq.5 in above equation, we get
$
   \Rightarrow {\text{time = }}\dfrac{{3k}}{k} \\
   \Rightarrow {\text{time = 3sec}}{\text{.}} \\
$
Hence, the time taken by the car to reach the foot of the tower from point B is 3sec.


Note:-Whenever you get this type of question the key concept to solve this is to visualise the question and draw actions of questions as shown in the above figure and put all information in it. Now using trigonometric angles and relations you can find the unknown variable.