Question

A stone of mass \[m\] tied to a string of length \[l\] is rotating along a circular path with constant speed \[v\]. What is the torque on the stone?

Answer 1

Hint: Uniform circular motion describes the movement of an object along a circular path with constant speed. Angular and tangential acceleration will be zero. Angular velocity and linear speed of the particle are always constant. The kinetic energy of the particle also remains constant. The net linear acceleration of the particle is always radially inwards. The magnitude of centripetal force remains constant. The magnitude of centripetal acceleration within a uniform circular motion is also constant. The examples of uniform circular motion are motion of the Earth around the Sun, second, minute and hour hands of the watch, motion of cyclists on a circular track, etc.

Formula used: \[T = r \times F\]
Where, \[T\]-Tension,\[r\]-radial direction, and \[F\]- the force acting on the mass.

Complete step-by-step solution:

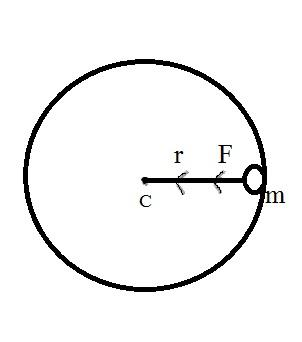
\[T = r \times F\]
Where, \[T\]-Tension,\[r\]-radial direction, and \[F\]- the force acting on the mass.
The radial direction would be from stone to center (\[c\]) of the circular path. \[F\] is the force acting on mass(\[m\]). We all know that, if the body is moving within a circular motion, definitely there’ll be a centrifugal force working along the center of the path.
Clearly, \[r\] and \[F\] working on the same axis or parallel to each other.
Finally, we can say that the net torques are zero.

Note: Torque is termed as the measure of the force that can cause an object to rotate about an axis. Force is what causes an object to accelerate within linear kinematics. Similarly, torque is what causes an angular acceleration. Hence, torque can be termed as the rotational equivalent of linear force. In physics, torque is solely the tendency of a force to turn or twist. Different terminologies like moment or moment of force are interchangeably used to describe torque.