Question

A stone is thrown horizontally under gravity with a speed of 10m/sec. Find the radius of curvature of its trajectory at the end of 3sec after motion began.
A. $10\sqrt{10}m$
B. $100\sqrt{10}m$
C. $\sqrt{10}m$
D. $100m$

Answer 1

Hint: Firstly you could find all components of velocity at time t=3s. Remember that the horizontal velocity is constant for a projectile at the vertical component that can be found using laws of motion. Then you could find the value of tangential velocity using them. Now find the normal acceleration at that particular point. Now you could simply substitute these in the expression of the radius of trajectory to find the answer.
Formula used:
Equation of motion,
$v=u+at$
The radius of curvature of trajectory,
$r=\dfrac{{{\left( {{v}_{t}} \right)}^{2}}}{{{a}_{n}}}$

Complete step-by-step solution
We are told that a stone is thrown horizontally under gravity at a speed of 10m/s. We are asked to find the radius of the curvature of the stone’s trajectory after 3s of its motion.
The motion can be represented by the diagram given below.

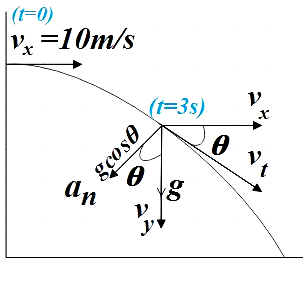
We are given the horizontal velocity as,
${{v}_{x}}=30m{{s}^{-1}}$ ……………………………… (1)
So at the beginning of the motion (t = 0), that is when the ball is being thrown horizontally, we only have the horizontal velocity for the ball, the vertical component of velocity is zero.
${{v}_{0y}}=0$
However, after 3secs, the ball develops a velocity along the vertical direction. Let this velocity be ${{v}_{y}}$ then, by Newton’s equations of motion we have,
${{v}_{y}}={{v}_{0y}}+gt$
$\Rightarrow {{v}_{y}}=0+\left( 10\times 3 \right)$
$\therefore {{v}_{y}}=30m{{s}^{-1}}$ …………………………………. (2)
At t = 3s, we also have a horizontal velocity with the same value as (1).
Now we could express the tangential velocity $\left( {{v}_{r}} \right)$ as the vector sum of the horizontal and vertical components of velocity. That is,
${{v}_{r}}=\sqrt{{{v}_{x}}^{2}+{{v}_{y}}^{2}}$
$\Rightarrow {{v}_{r}}=\sqrt{{{10}^{2}}+{{30}^{2}}}=\sqrt{1000}$
$\therefore {{v}_{r}}=10\sqrt{10}m{{s}^{-1}}$ ………………………………….. (3)
Now, recall that the radius of curvature of its trajectory (r) at any point of a projectile is given by,
$r=\dfrac{{{\left( {{v}_{t}} \right)}^{2}}}{{{a}_{n}}}$ ……………………………. (4)
Where, ${{v}_{t}}$ is the tangential velocity at that point and ${{a}_{n}}$ is the normal acceleration at that point.
From the figure, we see that the normal acceleration at $t=3s$is the horizontal component of g, that is,
${{a}_{N}}=g\cos \theta $
$\Rightarrow {{a}_{n}}=\left( 10m{{s}^{-2}} \right)\dfrac{{{v}_{x}}}{{{v}_{t}}}=10\left( \dfrac{10}{10\sqrt{10}} \right)$
$\therefore {{a}_{n}}=\sqrt{10}m{{s}^{-2}}$ …………………………. (5)
Substituting (5) in (4), we get,
$r=\dfrac{{{\left( 10\sqrt{10}m{{s}^{-1}} \right)}^{2}}}{\sqrt{10}m{{s}^{-2}}}$
$\therefore r=100\sqrt{10}m$
Therefore, we find the radius of curvature of the ball’s trajectory to be$100\sqrt{10}m$. Hence, the answer to the question is option B.

Note: It is really important to note while solving that the normal acceleration mentioned here is normal to the trajectory, that is, normal to the tangential velocity. Also, take the conventions used while substituting quantities like g. We have substituted +g as by convention g is positive downward.