Question

A stone is projected vertically up from the bottom of a water tank. Assuming no water resistance it will go up & come down in same time but if water drag is present then the time it takes to go up, ${t_{up}}$ and the time it takes to come down, ${t_{down}}$ are related as

Answer 1

Hint: Initially, they mentioned that the stone moved up and down at the same time. But, due to the water resistance, the time has changed. It is because water resistance is an opposition force acting in the direction opposite to the motion. We need to find the net acceleration in each direction, to understand the relation between the time taken in each case.
Formula used:
$\eqalign{
  & {a_{up}} = \dfrac{{ - ({F_{drag}} + mg)}}{m} \cr
  & {a_{down}} = \dfrac{{mg - {F_{drag}}}}{m} \cr} $

Complete answer:
It is given in the question, that initially, the body moves up and down at the same time when it is released vertically. But when the water drag is present the time taken to go up and to come down changes.

Let’s draw a free body diagram, to know the forces involved in the stone.

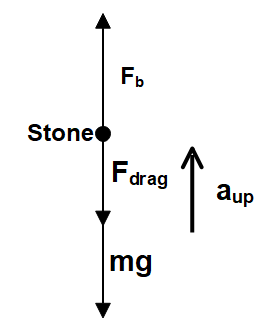
So, when the object is moving in an upward direction the weight mg in the downward direction and the water drag will also act in a downward direction while the buoyancy force is always upwards as shown in the free-body diagram of the stone. So, the acceleration of the stone can be given by
$\eqalign{
  & m{a_{up}} = {F_b} - ({F_{drag}} + mg) \cr
  & \Rightarrow {a_{up}} = \dfrac{{{F_b} - ({F_{drag}} + mg)}}{m} \cr} $
Similarly, the free body diagram of the stone moving in a downward direction is

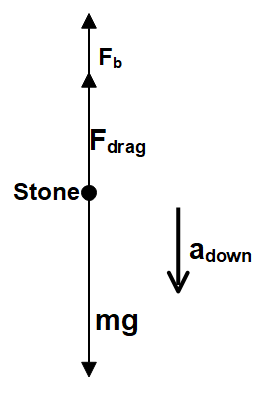
Here, while the stone is moving downward, the water drag acts upwards and the weight of the stone acts downwards and the buoyancy force acts in an upward direction. So, the acceleration of the stone while moving downwards is given by
$\eqalign{
  & m{a_{down}} = mg - ({F_{drag}} + {F_b}) \cr
  & \Rightarrow {a_{down}} = \dfrac{{mg - ({F_{drag}} + {F_b})}}{m} \cr} $
The buoyant force can be neglected because the volume occupied by the stone might be very small. Thus, we can write
$\eqalign{
  & {a_{up}} = \dfrac{{ - ({F_{drag}} + mg)}}{m} \cr
  & {a_{down}} = \dfrac{{mg - {F_{drag}}}}{m} \cr} $
You can see the obvious, $\left| {{a_{up}}} \right| > \left| {{a_{down}}} \right|$.
But acceleration is inversely proportional to time, so we have
$\eqalign{
  & \dfrac{1}{{{t_{up}}}} > \dfrac{1}{{{t_{down}}}} \cr
  & \therefore {t_{up}} < {t_{down}} \cr} $
Therefore, the time taken to go up is less than the time taken to come down by the stone.

Note:
Don’t confuse water drag for buoyancy force. Water drag is the opposition force applied by fluids, opposite to the relative motion of the object. It is also called water resistance. While buoyancy force is the force applied due to the pressure exerted by the fluid. It is always constant and upward in direction.