Question

A stick of length 10 units rests against the floor and a wall of a room. If the stick begins to slide on the floor then the locus of its middle point is:
\[\left( \text{a} \right)\text{ }{{x}^{2}}+{{y}^{2}}=2.5\]
\[\left( \text{b} \right)\text{ }{{x}^{2}}+{{y}^{2}}=25\]
\[\left( \text{c} \right)\text{ }{{x}^{2}}+{{y}^{2}}=100\]
(d) None of these

Answer 1

Hint: To solve the above question, we will first find out what a locus is. Then we will consider the floor as the x-axis and wall as the y-axis. We will assume that the mid-point has coordinates h and k. Also, we will assume that the point at which stick touches the floor is \[A\left( {{x}_{1}},0 \right)\] and the point at which stick touches the wall is \[B\left( 0,{{y}_{1}} \right).\] Then we will develop the relation between \[{{x}_{1}}\] and h and \[{{y}_{1}}\] and k. After doing this, we will determine the locus by applying the Pythagoras theorem in the triangle formed due to the stick, wall, and the floor.

Complete step-by-step solution -
Locus is the set of points that satisfy a certain property. Now, we have to determine the property of the midpoint of the stick when it starts sliding. Now we consider the floor as the x-axis and wall as the y-axis. The stick in the sliding position is drawn below.

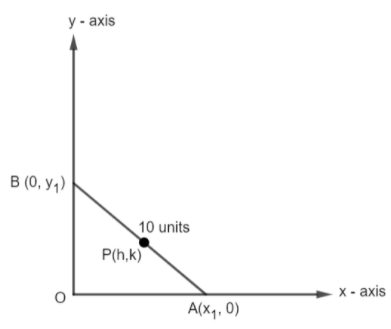
Now AB is the stick that is sliding and P is its midpoint. As point A touches the floor, it has y – coordinate as 0. Similarly, point B touches the wall, it has x – coordinate as 0. Now, P is the midpoint of stick AB. By midpoint formula, if there are two points E (a, b) and F (c, d), then its midpoint will be given by,
\[M\left( \alpha ,\beta \right)=\left( \dfrac{a+b}{2},\dfrac{c+d}{2} \right)\]
Similarly, we can say that,
\[P\left( h,k \right)=\left( \dfrac{{{x}_{1}}+0}{2},\dfrac{0+{{y}_{1}}}{2} \right)\]
\[\Rightarrow h=\dfrac{{{x}_{1}}}{2}.....\left( i \right)\]
\[\Rightarrow k=\dfrac{{{y}_{1}}}{2}.....\left( ii \right)\]
Now, we will apply the Pythagoras theorem in the right-angled triangle AOB. According to Pythagoras theorem, we can say that if H is the hypotenuse, B is the base and P is the perpendicular, then,
\[{{H}^{2}}={{P}^{2}}+{{B}^{2}}\]
In our case, H = AB, P = OB and B = OA. Thus, we have,
\[{{\left( AB \right)}^{2}}={{\left( OB \right)}^{2}}+{{\left( OA \right)}^{2}}\]
\[\Rightarrow {{\left( 10 \right)}^{2}}={{y}_{1}}^{2}+{{x}_{1}}^{2}\]
\[\Rightarrow {{x}_{1}}^{2}+{{y}_{1}}^{2}=100.....\left( iii \right)\]
From (i) and (ii), we have,
\[h=\dfrac{{{x}_{1}}}{2}\]
\[\Rightarrow {{x}_{1}}=2h.....\left( iv \right)\]
\[k=\dfrac{{{y}_{1}}}{2}\]
\[\Rightarrow {{y}_{1}}=2k.....\left( v \right)\]
Now, we will put the values of \[{{x}_{1}}\] and \[{{y}_{1}}\] from (iv) and (v) to (iii). Thus, we will get,
\[\Rightarrow {{\left( 2h \right)}^{2}}+{{\left( 2k \right)}^{2}}=100\]
\[\Rightarrow 4{{h}^{2}}+4{{k}^{2}}=100\]
\[\Rightarrow 4\left( {{h}^{2}}+{{k}^{2}} \right)=100\]
\[\Rightarrow {{h}^{2}}+{{k}^{2}}=\dfrac{100}{4}\]
\[\Rightarrow {{h}^{2}}+{{k}^{2}}=25\]
On putting h = x and k = y, we will get,
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=25\]
Hence, option (b) is the correct answer.

Note: Here, we have considered that the stick is present in two dimensions and as its slides, only x and y coordinates of the midpoint of the stick vary and z coordinate remains constant. Also, the locus obtained is a circle but the actual locus will only be the arc of the circle in the first quadrant.