Question

A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is \[60^\circ \] and from the same point the angle of elevation of the top of the pedestal is$45^\circ $. Find the height of the pedestal.
$
  {\text{A}}{\text{. Height of the pedestal = 0}}{\text{.2}}\left( {\sqrt 7 - 1} \right){\text{m}} \\
  {\text{B}}{\text{. Height of the pedestal = 0}}{\text{.8}}\left( {\sqrt 3 + 1} \right){\text{m}} \\
  {\text{C}}{\text{. Height of the pedestal = 1}}{\text{.6}}\left( {\sqrt 5 + 1} \right){\text{m}} \\
  {\text{D}}{\text{. Height of the pedestal = 1}}{\text{.9}}\left( {\sqrt {11} - 1} \right){\text{m}} \\
$

Answer 1

Hint: With respect to the data given in the question we draw an appropriate figure to help us with the solution. Observing the figure, we compute the tan of the given angles in the triangle to establish a relation which includes the height h. Then we solve the equation to find the answer.

Complete step by step answer:
Given Data, height of statue = 1.6m.
Angles of elevations to the statue and pedestal respectively are \[60^\circ \]and$45^\circ $.

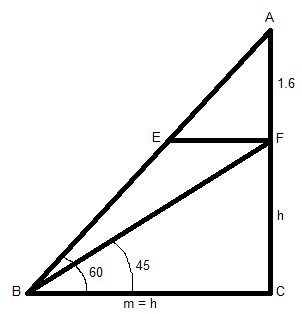
Let us consider a figure, a triangle ABC as shown which subtends an angle 60° with the ground BC and a triangle BFC which subtends an angle 45° with the ground BC. Let ‘h’ be the height of the pedestal as shown in the figure.
Where m is the horizontal distance between the point and the pedestal.
Now from the figure,
$
  \angle {\text{FBC = 45}}^\circ \\
  \angle {\text{ABC = 60}}^\circ \\
$
Therefore, applying tan function to this angle gives us
From triangle ∆FBC
⟹${\text{tan45}}^\circ {\text{ = }}\dfrac{{\text{h}}}{{\text{m}}} = 1{\text{ - - - - - - }}\left( {{\text{from trigonometric table of tan, tan45}}^\circ {\text{ = 1}}} \right)$
Hence h = m.
Also,
From triangle ∆ABC
$
  {\text{tan60}}^\circ {\text{ = }}\dfrac{{1.6{\text{ + h}}}}{{\text{h}}}{\text{ - - - - - }}\left( {{\text{from trigonometric table of tan, tan60}}^\circ {\text{ = }}\sqrt 3 } \right) \\
   \Rightarrow \sqrt 3 = {\text{ }}\dfrac{{1.6{\text{ + h}}}}{{\text{h}}} \\
   \Rightarrow \sqrt 3 {\text{h = 1}}{\text{.6 + h}} \\
   \Rightarrow {\text{1}}{\text{.6 = h}}\left( {\sqrt 3 - 1} \right) \\
   \Rightarrow {\text{h = }}\dfrac{{1.6}}{{\sqrt 3 - 1}} \\
    \\
$
Now we multiply $\sqrt 3 + 1$ on both numerator and denominator, we get
${\text{h = }}\dfrac{{1.6\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}{\text{ - - - - - }}\left( {{\text{we know (a + b)(a - b) = }}{{\text{a}}^2} - {{\text{b}}^2}} \right)$
$ \Rightarrow {\text{h = }}\dfrac{{1.6\left( {\sqrt 3 + 1} \right)}}{{3 - 1}} = \dfrac{{1.6}}{2}\left( {\sqrt 3 + 1} \right) = 0.8\left( {\sqrt 3 + 1} \right)$
⟹h = 2.185m.
Hence the height of the pedestal is $0.8\left( {\sqrt 3 + 1} \right)$m.

So, the correct answer is “Option B”.

Note: In order to solve this type of questions the key is to have a good understanding of the concepts of heights and distances. We make use of the properties of the figure to establish a relation. In case the given figure had an angle of 90°, we could have used Pythagoras theorem. Observing the data, one way or the other we have to make an equation to solve for the answer.