Question

A standard interior staircase is having steps each with a rise or the height of $19cm$ and a run or the horizontal depth of $23cm$. Research suggests that the stairs would be safer for descent if the run was $28cm$. For a specific staircase of height in total $4.57m$, how much farther into the room would the staircase extend when this much variation in run was produced?

Answer 1

Hint: Firstly we have to find how many staircases are required to reach the mentioned height. Then we have to find how much the stairs will extend in the room. The number of steps can be found by taking the ratio of total height to the height of the staircase. Multiply this number of steps with the horizontal depth of the stair.

Complete answer:
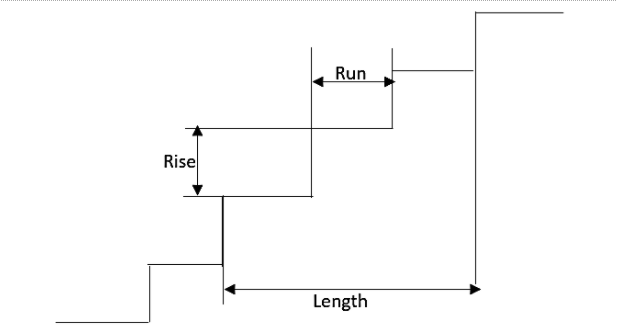
It has been given that the standard staircase height is,
${{S}_{h}}=19cm$
Standard staircase run is given as,
${{S}_{r}}=23cm$
The staircase run as per the suggestion given after the research is given as,
${{S}_{s}}=28cm$
Total height is given as,
$h=4.57m$
At first we have to find the number of steps required to reach this height. Therefore the number of steps will be,
$n=\dfrac{\text{total height}}{\text{staircase height}}$
Substituting the values in it will give,
$n=\dfrac{4.57\times 100cm}{19cm}=24\text{steps}$
From this we can understand that the staircase will be extended inside the room for the obtained value of the number of steps times the difference in the suggested and standard run. That is,
${{S}_{s}}-{{S}_{r}}=28-23=5cm$
Therefore we can calculate this such as,
$L=24\times 5cm=120cm=1.2m$
Hence the required answer for the question has been obtained.

Note: The units of the parameters given in the question should be taken care of well. Some of the quantities are given in centimetres and some are given in meters. The centimetre should be converted to a meter when we solve in order to make the value standardised.