Question

A square is inscribed in a circle of radius $R$, a circle is inscribed in the square, a new square in the circle, and so on for '$n$' times. Find the limit of the sum of areas of all the squares as $n\to \infty $.

Answer 1

Hint: We will look at a rough diagram to understand what is being asked in the question. We will find the length of the side of the first square in terms of $R$. Then we will find the length of the sides of subsequent squares that are inscribed into circles in terms of $R$. We will use the fact that the diagonal of a square is $\sqrt{2}\times \text{side length}$. Then we will calculate the areas of these squares. After that, we will find the sum of areas of all the squares as $n\to \infty $.

Complete step-by-step solution
Let us look at a rough diagram, which has the given circle and the first inscribed square in it.

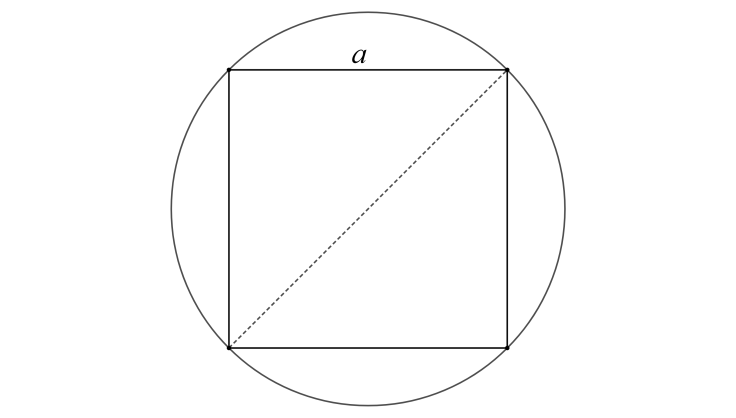
Let the side of the square be $a$. We know that the length of the diagonal of a square is $\sqrt{2}a$. Since this square is inscribed in a circle, the length of the diagonal of this square is equal to the diameter of the circle. So we have the following,
$\sqrt{2}a=2R$
Therefore, the side of the square in terms of the radius of the circle is
$a=\sqrt{2}R$
Now, we have to inscribe a circle inside the square with side length $a$.The diameter of this circle is equal to the side of this square. Let the radius of this circle be ${{r}_{1}}$. So, we have that ${{r}_{1}}=\dfrac{{{a}_{1}}}{2}$. The radius of this circle in terms of $R$ will be
${{r}_{1}}=\dfrac{\sqrt{2}R}{2}=\dfrac{R}{\sqrt{2}}$

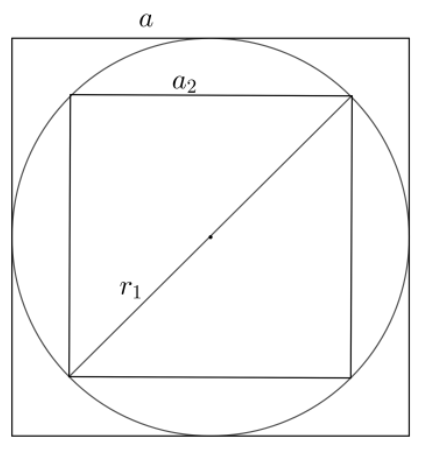
Now, we will inscribe a square of side length ${{a}_{2}}$ inside the circle with radius ${{r}_{1}}$. Using the relation between the diagonal of the square and the diameter of the circle, we get the following
$\sqrt{2}{{a}_{2}}=2{{r}_{1}}$
The value of ${{a}_{2}}$ in terms of $R$ can be obtained by substituting the value of ${{r}_{1}}$ in the following manner,
${{a}_{2}}=\sqrt{2}\times \dfrac{R}{\sqrt{2}}=R$
Now, again we will inscribe a circle inside the square of side length ${{a}_{2}}$. Let the radius of this circle be ${{r}_{2}}$. So, the diameter of this circle will be equal to the side length ${{a}_{2}}$. Therefore, we have the following,
$\begin{align}
  & 2{{r}_{2}}={{a}_{2}} \\
 & \Rightarrow 2{{r}_{2}}=R \\
 & \therefore {{r}_{2}}=\dfrac{R}{2} \\
\end{align}$
Next, we will inscribe a square of side length ${{a}_{3}}$ inside the circle with radius ${{r}_{2}}$. The diagonal of this square is equal to the diameter of the circle. Hence we get,
$\begin{align}
  & \sqrt{2}{{a}_{3}}=2{{r}_{2}} \\
 & \Rightarrow {{a}_{3}}=\sqrt{2}\times \dfrac{R}{2} \\
 & \therefore {{a}_{3}}=\dfrac{R}{\sqrt{2}} \\
\end{align}$
We have to continue this for '$n$' times. If we look at the sequence of sides of the inscribed squares, we have ${{a}_{1}},{{a}_{2}},{{a}_{3}},\ldots $. In terms of $R$, the sequence is $\sqrt{2}R,R,\dfrac{R}{\sqrt{2}},\ldots $. The area of a square is given by $A={{\left( \text{side} \right)}^{2}}$. So, the sequence of areas of the squares will look like ${{\left( \sqrt{2}R \right)}^{2}},{{R}^{2}},{{\left( \dfrac{R}{\sqrt{2}} \right)}^{2}},\ldots $ which is equal to is $2{{R}^{2}},{{R}^{2}},\dfrac{{{R}^{2}}}{2},\ldots $. This sequence is a geometric progression with the first term as $2{{R}^{2}}$ and the common ratio as $\dfrac{1}{2}$. Since the common ratio is less than 1, we can write the sum of this series as $n\to \infty $ in the following manner,
$\begin{align}
& S=\dfrac{a}{1-r}
& S=\dfrac{2{{R}^{2}}}{1-\dfrac{1}{2}} \\
 & \Rightarrow S=2\times 2{{R}^{2}} \\
 & \therefore S=4{{R}^{2}} \\
\end{align}$
So, the limit of the sum of areas of the inscribed squares as $n\to \infty $ is $4{{R}^{2}}$.

Note: In this type of question, it is important that we are able to discern the pattern of the sequence of values we obtain at every step. It is useful to know the concept of geometric progression and its formulae. The key aspect in this is the relation between the diameter of the circle and the diagonal of its inscribed square.