Question

A square and an equilateral triangle have equal perimeters. If the diagonal of the square is $12\sqrt 2 cm$then area of the triangle is
A. $24\sqrt 2 c{m^2}$
B. $24\sqrt 3 c{m^2}$
C. $48\sqrt 3 c{m^2}$
D. $64\sqrt 3 c{m^2}$

Answer 1

Hint-In this question square and triangle have the same perimeter. Find the relation between their sides. Calculate the side of the square first. Find the area of the triangle directly using the basic formula of area of equilateral triangle and the relation obtained.

Complete step by step answer:

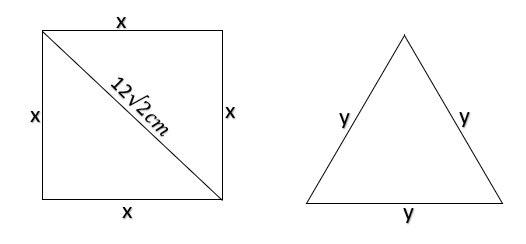
Let side of square be $x$units
Side of equilateral triangle be $y$ units
Given, both have equal perimeters
$ \Rightarrow 4x = 3y$
Diagonal of square = $12\sqrt 2 $
Using Pythagoras theorem
$
  {x^2} + {x^2} = {(12\sqrt 2 )^2} \\
  2{x^2} = 144 \times 2 \\
  {x^2} = 144 \\
  x = 12{\text{ units}} \\
    \\
   \Rightarrow y = \dfrac{4}{3}x = \dfrac{4}{3} \times 12 = 16{\text{ units}} \\
  {\text{Area of equilateral triangle = }}\dfrac{{\sqrt 3 }}{4}{\left( y \right)^2} \\
   = \dfrac{{\sqrt 3 }}{4} \times 16 \times 16 \\
   = 64\sqrt 3 c{m^2} \\
$
Therefore, the area of triangle is $64\sqrt 3 c{m^2}$
Note- In order to solve such problems students must start with considering the sides of the given geometrical figures in terms of some unknown variable. Also, students must remember the formula for the area and the perimeter for some common geometrical figures, some of them are mentioned in the solution.