Question

A spherical watermelon of radius $4cm$is halved. The uniform width of the white part surrounding the red edible part is $1cm$. From half of the melon, the red part of the fruit is scooped out. Taking $\pi = 3.14$, find
i) The volume of the edible part of the fruit taken out (ignore the volume of seeds).
ii) The surface area of the white part of the hemispherical piece.

Answer 1

Hint: First, we need to analyze the given information and we have to draw an appropriate diagram that shows the given information. Here, we are asked to calculate the volume of the red edible part of the watermelon and the surface area of the white part of the hemispherical piece.

Formula to be used:
a) The formula to calculate the volume of the hemisphere is as follows.
The volume of a hemisphere, $V = \dfrac{2}{3}\pi {r^3}$
Where$r$is the radius of the hemisphere.
b) The formula to calculate the area of the circle is as follows.
Area of the circle, $A = \pi {r^2}$
Where$r$is the radius of the circle.
c) The formula to calculate the curved surface area of the hemisphere is as follows.
The curved surface area of the hemisphere $ = 2\pi {r^2}$
Where$r$is the radius of the hemisphere.

Complete step by step answer:
Let OA be the radius of the hemisphere and AB be the width of the white part.
It is given that the radius of the hemisphere, $OA = 4cm$ and the radius of the white part,$AB = 1cm$

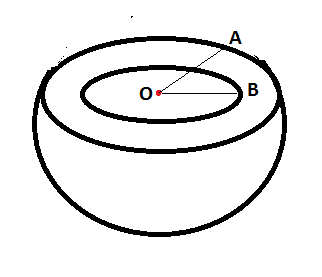
Now, we shall find the radius of the edible part OB.
The radius of the edible part $OB = OA - AB$
$OB = 4 - 1$ $ \Rightarrow OB = 3cm$
i. We are asked to calculate the volume of the edible part of the fruit taken out.
The volume of the edible part$ = $Volume of the outer hemisphere$ - $Volume of the inner hemisphere
                                               \[ = \dfrac{2}{3}\pi {\left( {OA} \right)^3} - \dfrac{2}{3}\pi {\left( {OB} \right)^3}\]
                                              \[ = \dfrac{2}{3}\pi {\left( 4 \right)^3} - \dfrac{2}{3}\pi {\left( 3 \right)^3}\]
                                              \[ = \dfrac{2}{3}\pi \left( {64} \right) - \dfrac{2}{3}\pi \left( {27} \right)\]
                                              \[ = \dfrac{2}{3}\pi \left( {64 - 27} \right)\]
                                               \[ = \dfrac{2}{3} \times 3.14 \times 37\]
                                               $ = 77.453c{m^3}$
Hence, the volume of the edible part is$77.453c{m^3}$
ii. We are asked to calculate the surface area of the white part.
The area of the white part$ = $Area of the circle with radius OA$ - $ Area of the circle with radius OB
                                               $ = \pi {\left( {OA} \right)^2} - \pi {\left( {OB} \right)^2}$
                                               $ = \pi {\left( 4 \right)^2} - \pi {\left( 3 \right)^2}$
                                               $ = 16\pi - 27\pi $
                                                $ = 7\pi $
                                                $
   = 7 \times 3.14 \\
   = 21.98c{m^2} \\
 $
Now, the surface area of the white part $ = $ area of the white part $ + $ area of the inner surface of the sphere with radius OB
Here, the area of the inner surface of the sphere is nothing but the curved surface of the hemisphere
Hence using the formula, we have
The surface area of the white part$ = 21.98 + 2\pi {\left( 3 \right)^2}$
                                                              $ = 21.98 + 2 \times 3.14 \times 9$
                                                              $ = 21.98 + 56.52$
                                                              $ = 78.5c{m^2}$
Therefore the surface area of the white part$ = 78.5c{m^2}$
Note: We have drawn a figure using the given information. Also, we need to know the appropriate formula so that we are able to solve the problem. Hence, the volume of the edible part is $77.453c{m^3}$ and the surface area of the white part $ = 78.5c{m^2}$