Question

A spherical mirror produces an image of magnification -1 on a screen placed at a distance of 50cm from the mirror.
a) Write the type of mirror.
b) Find the distance of the object from the mirror.
c) What is the focal length of the mirror?
d) Draw the ray diagram to show the image formation of this case.

Answer 1

Hint: As the linear magnification is $-1$ so the mage distance is equal to the object distance. Use the mirror formula to calculate the focal length of the mirror.

Complete step by step solution:
The diagram below simplifies the situation for the above problem:

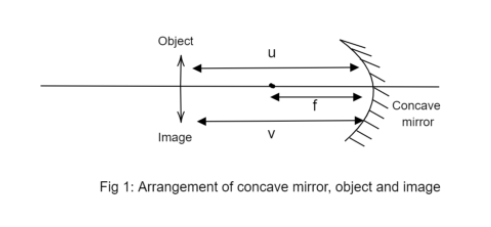
As the magnification produced by the mirror is negative. So the mirror is a concave mirror because only a concave mirror can produce an image with negative magnification.

Step1: writing down what is given and what needs to be calculated

Image distance,$v =- 50cm$ (as mirror is concave)
Magnification $m =- 1$
Object distance $u = ?$
Focal length $f = ?$

Step2: apply the magnification equation to calculate the object distance.
Therefore,
Also
$m =- \dfrac{v}{u}$
$ - 1 =- \dfrac{{( - 50)}}{u} $
$ \Rightarrow u =- 50cm $
Step3: Now use the mirror formula to calculate the focal length-
$\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v}$
Substitute all the values in above equation we get,
$\dfrac{1}{f} = \dfrac{1}{{( - 50)}} + \dfrac{1}{{( - 50)}} $
$ \Rightarrow \dfrac{1}{f} =- \dfrac{1}{{50}} - \dfrac{1}{{50}} $
On simplifying the above equation, we get
$ \dfrac{1}{f} =- \dfrac{2}{{50}} $
On further calculations,
$\dfrac{1}{f} =- \dfrac{1}{{25}} $
$ \Rightarrow f =- 25cm $
This is the required focal length of the mirror.
(d) Figure 2: Image formation diagram:

$\therefore$ The given mirror is a concave mirror.
The distance of the object from the mirror is $u=50cm$
The focal length of the mirror is $f=-25cm$

Note:
If magnification is unity then always object distance and image distance are equal in magnitude. Try to remember the mirror formula and the magnification equation.
In such kinds of problems, most care is taken while applying the sign conventions that we follow. We can select our own sign convention. But we have to be consistent throughout Sign Convention:
1. The Mirror center to be the origin.
2. The left of the mirror is negative right positive.
3. Above principle axis positive and below negative.