Question

A sphere rolls down on an inclined plane of inclination \[\theta \]. What is the acceleration as the sphere reaches the bottom?
A. \[\dfrac{5}{7}g\sin \theta \]
B. \[\dfrac{3}{5}g\sin \theta \]
C. \[\dfrac{2}{7}g\sin \theta \]
D. \[\dfrac{2}{5}g\sin \theta \]

Answer 1

Hint:Use the expression for Newton’s second law of motion. Apply Newton’s second law in horizontal direction to the sphere. Derive an expression for the torque acting on the sphere due to the frictional force and hence derive the expression for frictional force. Substitute the expression derived for frictional force in the expression for Newton’s second law and determine the required acceleration of the sphere.

Formulae used:
The expression for Newton’s second law of motion is
\[{F_{net}} = ma\] …… (1)
Here, \[{F_{net}}\] is the net force on the object, \[m\] is mass of the object and \[a\] is acceleration of the object.
The acceleration \[a\] of an object is
\[a = R\alpha \] …… (2)
Here, \[R\] is the radius of the object and \[\alpha \] is the angular acceleration of the object.
The torque \[\tau \] acting on an object due to a force \[F\] is
\[\tau = Fr\] …… (3)
Here, \[r\] is the perpendicular distance between point of action of the force and centre of torque.
The torque \[\tau \] acting on an object is
\[\tau = I\alpha \] …… (4)
Here, \[I\] is the momentum of inertia of the object and \[\alpha \] is the angular acceleration of the object.
The moment of inertia \[I\] of a solid sphere about an axis passing through its centre is
\[I = \dfrac{2}{5}M{R^2}\] …… (5)
Here, \[M\] is the mass of the sphere and \[R\] is the radius of the sphere.

Complete step by step answer:
We have given that a sphere is rolling down an inclined plane having inclination \[\theta \] of with the horizontal. Let \[m\] be the mass of the sphere and \[a\] be the acceleration of the sphere down the inclined plane.Let us draw the free body diagram of the sphere.

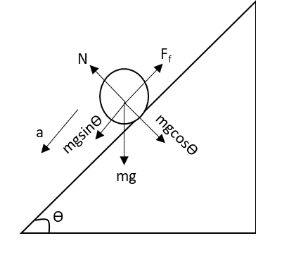
In the above free body diagram, \[mg\] is the weight of the sphere, \[{F_f}\] is the frictional force acting on the sphere and \[N\] is the normal force on the sphere by the inclined plane. The components of weight acting on the sphere are shown in the above diagram.
Apply Newton’s second law of motion to the sphere in horizontal direction.
\[mg\sin \theta - {F_f} = ma\] …… (6)
As the sphere is rolling, there must be a torque acting on the sphere.
Rewrite equation (3) for the torques due to frictional force.
\[\tau = {F_f}R\]
Here, \[R\] is the radius of the sphere.
Substitute \[I\alpha \] for \[\tau \] in the above equation.
\[I\alpha = {F_f}R\]
Substitute \[\dfrac{2}{5}m{R^2}\] for \[I\] and \[\dfrac{a}{R}\] for \[\alpha \] in the above equation.
\[\dfrac{2}{5}M{R^2}\dfrac{a}{R} = {F_f}R\]
\[ \Rightarrow \dfrac{2}{5}ma = {F_f}\]
\[ \Rightarrow {F_f} = \dfrac{2}{5}ma\]
Substitute \[\dfrac{2}{5}ma\] for \[{F_f}\] in equation (6).
\[mg\sin \theta - \dfrac{2}{5}ma = ma\]
\[ \Rightarrow a + \dfrac{2}{5}a = g\sin \theta \]
\[ \Rightarrow \dfrac{7}{5}a = g\sin \theta \]
\[ \therefore a = \dfrac{5}{7}g\sin \theta \]
Therefore, the acceleration of the sphere when it reaches the bottom of the inclined plane is \[\dfrac{5}{7}g\sin \theta \].

Hence, the correct option is A.

Note:One can also solve the same question by another way. Use the formula for the acceleration of an object rolling down on an inclined plane. Substitute the value of radius of gyration for the sphere in this formula and derive the final answer for the acceleration of the sphere when it reaches at the bottom of the inclined plane.