Question

A sphere of diameter $6\,cm$ is dropped in a right circular cylindrical vessel partly filled with water. The diameter of the cylindrical vessel is $13\,cm.$If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel.

Answer 1

Hint: The volume of the sphere will be equal to the volume of the water that raised from the original height that the cylinder had, before dropping the sphere. Compare the volume of the raised water with the volume of the sphere to solve the question.

Complete Step by Step Solution:
It is given to us that,
The sphere has diameter, $d = 6\,cm$
Thus the radius of the cylinder is $r = 3\,cm$
The diameter of right circular cylindrical vessel is $D = 13\,cm.$
Thus the radius of the circular cylindrical vessel is $R = \dfrac{{13}}{2}\,cm$
Observe the diagram

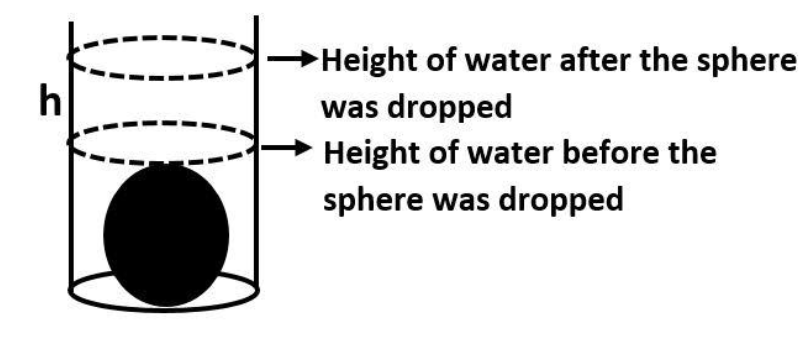
Let the height of the rise in water level be $'h'.$
Now, we can observe that the volume of water that will rise from its initial level will be equal to the volume of the sphere.
Therefore, ${V_c} = {V_s}$ . . . (1)
Where,
${V_c}$ is the volume of the water level raised.
${V_s}$ is the volume of the sphere.
Now, we know that,
${V_c} = \pi {R^2}h$ and ${V_s} = \dfrac{4}{3}\pi {r^3}$
Therefore, from equation (1), we get
$\Rightarrow \pi {R^2}h = \dfrac{4}{3}\pi {r^3}$
Substitute the given values in the above equation. We get
$\Rightarrow {\left( {\dfrac{{13}}{2}} \right)^2} \times h = \dfrac{4}{3} \times {(3)^3}$
By simplifying it, we get
$\Rightarrow \dfrac{{13 \times 13}}{4} \times h = \dfrac{4}{3} \times 3 \times 3 \times 3$
$\Rightarrow h = \dfrac{{4 \times 3 \times 3 \times 3 \times 4}}{{13 \times 13}}$
$\Rightarrow h = \dfrac{{144}}{{169}} = 0.83$

Therefore, the rise in water level will be $0.83\,cm$

Note:
In this question, you need to understand that the water level of the cylindrical vessel will rise. And that the volume of the raised water will be equal to the volume of the cylinder. Without understanding this reasoning, you will never be able to solve this question. But once you understand this, then this question is a simple question of substituting values in the formula, and to get the answer.