Answer
Verified373.3k+ views
Hint: Directly consider the volume of water level raised in terms of cylindrical vessel’s volume of height equal to water level raised. It can easily be equated with the volume of the sphere to calculate the diameter of a cylindrical vessel.
Complete step-by-step answer:
Here, as per the given conditions, a sphere of diameter = 12cm is submerged into a cylindrical vessel partly filled with water, after sphere is dropped in vessel the water level rises by $3\dfrac{5}{9}cm$, i.e.,
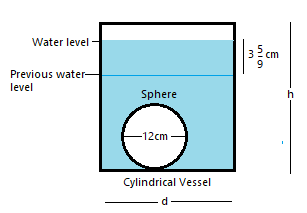
Let’s say, height of cylinder be $h$cm and diameter of cylindrical vessel be $d$cm, or radius of cylindrical vessel be $\dfrac{d}{2}={{r}_{c}}$cm and diameter of sphere is $12cm$, or radius of sphere = ${{r}_{s}}=\dfrac{12}{2}=6cm$.
Since the volume of water inside the cylindrical vessel remains the same, the rise in water level is definitely caused by an additional volume of sphere. Thus, we can say that
$\Rightarrow $ Volume of water raised = volume of sphere submerged into the cylindrical vessel, i.e.,
$\Rightarrow $ Volume of cylinder with height, ${{h}_{waterlevel}}=\left( 3\dfrac{5}{9} \right)cm$ with radius $\left( {{r}_{c}} \right)$cm = volume of sphere of radius$\left( {{r}_{s}} \right)cm$, or
$\Rightarrow \pi {{r}_{c}}^{2}{{h}_{waterlevel}}=\dfrac{4}{3}\pi {{r}_{s}}^{3}$
Substituting the given values in the above equation, we get
$\begin{align}
& \Rightarrow \pi {{r}_{c}}^{2}{{h}_{waterlevel}}=\dfrac{4}{3}\pi {{r}_{s}}^{3} \\
& \Rightarrow \pi {{r}_{c}}^{2}\left( 3\dfrac{5}{9} \right)=\dfrac{4}{3}\pi {{\left( 6 \right)}^{3}} \\
\end{align}$
Cancelling out the $\pi $ from both sides, we get
\[\begin{align}
& \Rightarrow \pi {{r}_{c}}^{2}\left( 3\dfrac{5}{9} \right)=\dfrac{4}{3}\pi {{\left( 6 \right)}^{3}} \\
& \Rightarrow {{r}_{c}}^{2}\left( \dfrac{32}{9} \right)=\dfrac{4}{3}\left( 216 \right) \\
& \Rightarrow {{r}_{c}}^{2}\left( \dfrac{32}{9} \right)=4\times 72 \\
& \Rightarrow {{r}_{c}}^{2}\left( \dfrac{32}{9} \right)=288 \\
\end{align}\]
On cross-multiplication, we get
\[\begin{align}
& \Rightarrow {{r}_{c}}^{2}\left( \dfrac{32}{9} \right)=288 \\
& \Rightarrow {{r}_{c}}^{2}=\dfrac{288\times 9}{32} \\
& \Rightarrow {{r}_{c}}^{2}=81 \\
\end{align}\]
Taking square root on both the sides, we get
\[\begin{align}
& \Rightarrow {{r}_{c}}^{2}=81 \\
& \Rightarrow \sqrt{{{r}_{c}}^{2}}=\sqrt{81} \\
& \Rightarrow {{r}_{c}}=9cm \\
\end{align}\]
As, ${{r}_{c}}$ cannot have negative value, so ${{r}_{c}}=-9cm$ is neglected.
Hence, the diameter of the cylindrical vessel = ${{d}_{c}}=2\times {{r}_{c}}=2\times 9=18cm$.
Note: There is no size comparison given for the cylindrical vessel and the sphere. So, a common mistake which can be committed by the student is by getting confused and taking the sphere’s diameter equal to the diameter of the cylindrical vessel. Another mistake can be substituting the diameter instead of the radius in the formula to find the volume.
Complete step-by-step answer:
Here, as per the given conditions, a sphere of diameter = 12cm is submerged into a cylindrical vessel partly filled with water, after sphere is dropped in vessel the water level rises by $3\dfrac{5}{9}cm$, i.e.,
Let’s say, height of cylinder be $h$cm and diameter of cylindrical vessel be $d$cm, or radius of cylindrical vessel be $\dfrac{d}{2}={{r}_{c}}$cm and diameter of sphere is $12cm$, or radius of sphere = ${{r}_{s}}=\dfrac{12}{2}=6cm$.
Since the volume of water inside the cylindrical vessel remains the same, the rise in water level is definitely caused by an additional volume of sphere. Thus, we can say that
$\Rightarrow $ Volume of water raised = volume of sphere submerged into the cylindrical vessel, i.e.,
$\Rightarrow $ Volume of cylinder with height, ${{h}_{waterlevel}}=\left( 3\dfrac{5}{9} \right)cm$ with radius $\left( {{r}_{c}} \right)$cm = volume of sphere of radius$\left( {{r}_{s}} \right)cm$, or
$\Rightarrow \pi {{r}_{c}}^{2}{{h}_{waterlevel}}=\dfrac{4}{3}\pi {{r}_{s}}^{3}$
Substituting the given values in the above equation, we get
$\begin{align}
& \Rightarrow \pi {{r}_{c}}^{2}{{h}_{waterlevel}}=\dfrac{4}{3}\pi {{r}_{s}}^{3} \\
& \Rightarrow \pi {{r}_{c}}^{2}\left( 3\dfrac{5}{9} \right)=\dfrac{4}{3}\pi {{\left( 6 \right)}^{3}} \\
\end{align}$
Cancelling out the $\pi $ from both sides, we get
\[\begin{align}
& \Rightarrow \pi {{r}_{c}}^{2}\left( 3\dfrac{5}{9} \right)=\dfrac{4}{3}\pi {{\left( 6 \right)}^{3}} \\
& \Rightarrow {{r}_{c}}^{2}\left( \dfrac{32}{9} \right)=\dfrac{4}{3}\left( 216 \right) \\
& \Rightarrow {{r}_{c}}^{2}\left( \dfrac{32}{9} \right)=4\times 72 \\
& \Rightarrow {{r}_{c}}^{2}\left( \dfrac{32}{9} \right)=288 \\
\end{align}\]
On cross-multiplication, we get
\[\begin{align}
& \Rightarrow {{r}_{c}}^{2}\left( \dfrac{32}{9} \right)=288 \\
& \Rightarrow {{r}_{c}}^{2}=\dfrac{288\times 9}{32} \\
& \Rightarrow {{r}_{c}}^{2}=81 \\
\end{align}\]
Taking square root on both the sides, we get
\[\begin{align}
& \Rightarrow {{r}_{c}}^{2}=81 \\
& \Rightarrow \sqrt{{{r}_{c}}^{2}}=\sqrt{81} \\
& \Rightarrow {{r}_{c}}=9cm \\
\end{align}\]
As, ${{r}_{c}}$ cannot have negative value, so ${{r}_{c}}=-9cm$ is neglected.
Hence, the diameter of the cylindrical vessel = ${{d}_{c}}=2\times {{r}_{c}}=2\times 9=18cm$.
Note: There is no size comparison given for the cylindrical vessel and the sphere. So, a common mistake which can be committed by the student is by getting confused and taking the sphere’s diameter equal to the diameter of the cylindrical vessel. Another mistake can be substituting the diameter instead of the radius in the formula to find the volume.
Recently Updated Pages
How many sigma and pi bonds are present in HCequiv class 11 chemistry CBSE
Mark and label the given geoinformation on the outline class 11 social science CBSE
When people say No pun intended what does that mea class 8 english CBSE
Name the states which share their boundary with Indias class 9 social science CBSE
Give an account of the Northern Plains of India class 9 social science CBSE
Change the following sentences into negative and interrogative class 10 english CBSE