Question

A sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then:

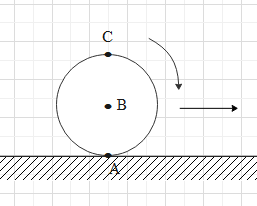
(This question has multiple correct options)
$\text{A}\text{. }\overrightarrow{{{V}_{C}}}-\overrightarrow{{{V}_{A}}}=2\left( \overrightarrow{{{V}_{B}}}-\overrightarrow{{{V}_{C}}} \right)$
$\text{B}\text{. }\overrightarrow{{{V}_{C}}}-\overrightarrow{{{V}_{B}}}=\overrightarrow{{{V}_{B}}}-\overrightarrow{{{V}_{A}}}$
$\text{C}\text{. }\left| \overrightarrow{{{V}_{C}}}-\overrightarrow{{{V}_{A}}} \right|=2\left| \overrightarrow{{{V}_{B}}}-\overrightarrow{{{V}_{C}}} \right|$
$\text{D}\text{. }\left| \overrightarrow{{{V}_{C}}}-\overrightarrow{{{V}_{A}}} \right|=4\left| \overrightarrow{{{V}_{B}}}-\overrightarrow{{{V}_{C}}} \right|$

Answer 1

Hint: In this case, the velocity of every will be due to the rotational motion and the translation motion of the sphere. Due to translation motion, each point will have a horizontal velocity v in the direction of x-axis. Due to the rotational motion, each point will have velocity given by $\overrightarrow{v}=\overrightarrow{r}\times \overrightarrow{\omega }$, where $\overrightarrow{r}$ is the position vector of the point from the centre of the sphere.

Formula used:
$\overrightarrow{v}=\overrightarrow{r}\times \overrightarrow{\omega }$

Complete answer:
Suppose the sphere of radius R is rotating about its centre (i.e. point B) with an angular velocity $\omega $. The sphere is moving forward with velocity v (meaning it has a translation motion.)
It is given that the sphere is rolling without slipping on a fixed horizontal plane surface. The condition for rolling without slipping is that the net velocity of the point of the sphere that is in contact with the plane surface (in this case, it is point A) must be equal to zero.
This means that $\overrightarrow{{{V}_{A}}}=0$

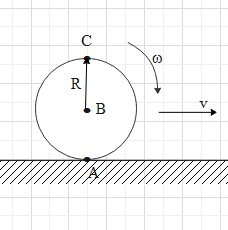
In this case, the velocity of every will be due to the rotational motion and the translation motion of the sphere.
Due to translation motion, each point will have a horizontal velocity v in the direction of x-axis.
i.e. $v\widehat{i}$.
Due to the rotational motion, each pint will have velocity given by $\overrightarrow{v}=\overrightarrow{r}\times \overrightarrow{\omega }$, where $\overrightarrow{r}$ is the position vector of the point from the centre of the sphere.
Here, the direction of $\overrightarrow{\omega }$ is in the direction of $\widehat{k}$.
Therefore, $\overrightarrow{{{V}_{C}}}=v\widehat{i}+\left( \overrightarrow{{{r}_{C}}}\times \overrightarrow{\omega } \right)$.
$\Rightarrow \overrightarrow{{{V}_{C}}}=v\widehat{i}+{{r}_{C}}\omega \widehat{i}$
Here, ${{r}_{C}}=R$.
$\Rightarrow \overrightarrow{{{V}_{C}}}=v\widehat{i}+R\omega \widehat{i}=\left( v+R\omega \right)\widehat{i}$
And
$\overrightarrow{{{V}_{B}}}=v\widehat{i}+\left( \overrightarrow{{{r}_{A}}}\times \overrightarrow{\omega } \right)$.
But $\overrightarrow{{{r}_{A}}}=0$.
$\Rightarrow \overrightarrow{{{V}_{B}}}=v\widehat{i}+0=v\widehat{i}$.
Similarly, we get that $\Rightarrow \overrightarrow{{{V}_{A}}}=\left( v-R\omega \right)\widehat{i}$
But $\overrightarrow{{{V}_{A}}}=0$.
$\Rightarrow \left( v-R\omega \right)=0$
$\Rightarrow v=R\omega $.
Therefore,
$\Rightarrow \overrightarrow{{{V}_{C}}}=2v\widehat{i}$
Now if we check the options, then the correct equations are
$\overrightarrow{{{V}_{C}}}-\overrightarrow{{{V}_{B}}}=\overrightarrow{{{V}_{B}}}-\overrightarrow{{{V}_{A}}}=v\widehat{i}$
And
$\left| \overrightarrow{{{V}_{C}}}-\overrightarrow{{{V}_{A}}} \right|=2\left| \overrightarrow{{{V}_{B}}}-\overrightarrow{{{V}_{C}}} \right|=2v$.
So, the correct answer is “Option B and C”.

Note:
Some students may write option A as the correct option. However, it is not.
$\overrightarrow{{{V}_{C}}}-\overrightarrow{{{V}_{A}}}=2v\widehat{i}-0=2v\widehat{i}$
And
$2\left( \overrightarrow{{{V}_{B}}}-\overrightarrow{{{V}_{C}}} \right)=2\left( v\widehat{i}-2v\widehat{i} \right)=2\left( -v\widehat{i} \right)=-2v\widehat{i}$
Therefore,
$\overrightarrow{{{V}_{C}}}-\overrightarrow{{{V}_{A}}}\ne 2\left( \overrightarrow{{{V}_{B}}}-\overrightarrow{{{V}_{C}}} \right)$.
Hence, option A is incorrect.