Question

A source of a sound is emitting sound waves in all directions in an absorption less medium. This source is at a distance of 4 m and 16m from points x and y respectively. The ratio of amplitude of waves at points x and y will be
A) 2:4
B) 4:1
C) 4:2
D) 1:4

Answer 1

Hint: We know that sound travels in a form of have from one medium to another. Here we have given a source which is emitting sound in all directions and its distance with respect to any random point x and y is 4 m and 16 m respectively. We have to find the ratio of amplitude at these points x and y.
Formula used:
\[{{A}_{r}}=\dfrac{A}{r}\]

Complete answer:
Sound waves are the waves which propagate sound energy from one medium to another. Like other waves sound has amplitude which decreases with the distance it travels, therefore when we move away from a source emitting sound waves gradually its intensity decreases and we hear feeble sound or at certain distance we can’t hear the sound which is emitted by the source. Sound waves are also absorbed while travelling from one medium to another or in some cases it is blocked.
According to the question, the source s is emitting sound waves in all directions and the medium in which it is propagating is absorption less and there are two points x and y at some distance from source with respect to which we have to find the amplitude of the sound wave.

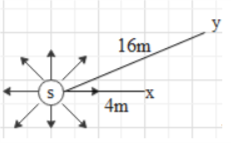
Now, the amplitude of sound wave at any reference point which is placed at distance r from the source is given as
\[{{A}_{r}}=\dfrac{A}{r}\]
Where A is the amplitude of a sound wave which is emitted from the source.
So the amplitude of sound wave at point x which is 4 m away from the source will be given as
\[{{A}_{x}}=\dfrac{A}{4}\text{ }.....................\text{(i)}\]
And the amplitude of sound wave at point y which is 16 m away is given as
\[{{A}_{y}}=\dfrac{A}{16}\text{ }.....................\text{(ii)}\]
Hence the ratio of amplitude of waves at points x and y using equation (i) and (ii) will be given as
\[\begin{align}
  & \dfrac{{{A}_{x}}}{{{A}_{y}}}=\dfrac{\dfrac{A}{4}}{\dfrac{A}{16}} \\
 & \Rightarrow \dfrac{{{A}_{x}}}{{{A}_{y}}}=\dfrac{16}{4} \\
 & \Rightarrow \dfrac{{{A}_{x}}}{{{A}_{y}}}=\dfrac{4}{1} \\
\end{align}\]

As we can see the ratio is 4:1, therefore option B is the correct answer.

Note:
In case the medium was not absorption less then while travelling the sound waves would have been absorbed in the way and then we would not be able to apply the formula we used. As due to absorption of the wave the energy will be decreased and so the amplitude of the wave will be decreased.