Question

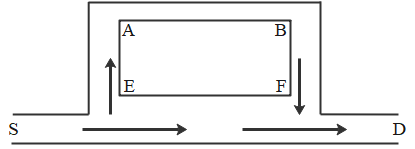
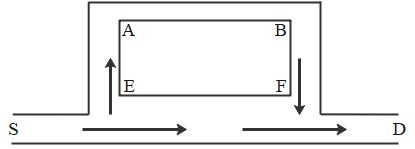
A sound wave starting from source S, follows two paths SEFD and SEABFD. If AB =$l$, AE = BF = $0.6l$ and wavelength of wave is $\lambda=6m$. If maximum sound is heard at D, then what is the minimum value of length $l$?

A. $11m$
B. $6m$
C. $2.5m$
D. $5m$

Answer 1

Hint: This question is related to interference of sound waves. The wave generated from source S travels different paths and interferes at D. We will use the condition of constructive interference to obtain value of length $l$.

Formula used:
For maxima $\Delta x=\pm n\lambda $ where $n$ is an integer.

Complete step by step answer:
When waves from two coherent sources superimpose, interference occurs. Where both waves interfere constructively, maximum is observed and where the waves interfere destructively minimum is obtained. Interference will be constructive or destructive depending on the path difference between the waves.
If path difference between the waves is an integral multiple of wavelength then both waves interfere constructively and maximum is obtained and if path difference is an odd multiple of half of the wavelength, both waves interfere destructively and minima is obtained. Mathematically,
For maxima $\Delta x=\pm n\lambda $ where $n$ is an integer.
For minima $\Delta x=\dfrac{\left( 2n\pm 1 \right)}{2}\lambda $ where $n$ is an integer.
As given, both the waves originated from the same source but travel different path lengths and interfere at D. Wave travelling along path SEABFD will travel more distance as compared to wave travelling along SEFD. Since at D maximum sound is heard, it means both waves have interfered constructively.

Path length difference between wave travelling along path SEABFD and wave travelling along SEFD is
$\Delta x=SEABFD-SEFD=\left( SE+EA+AB+BF+FD \right)-\left( SE+EF+FD \right)$
Since, $AB=EF$ and $AE=BF$, we have
$\Delta x=EA+BF$
It is given that, AE = BF = $0.6l$. Therefore,
$\Delta x=0.6l+0.6l=1.2l$
Applying the condition of maxima, we get
$1.2l=\pm n\lambda $
Wavelength of wave is $\lambda=6m$ and for minimum value of $l$, $n=\pm 1$. Applying these in above equation, we get
$1.2l=6m$
This implies that
$l=\dfrac{6}{1.2}=5m$
Therefore, option D is correct.

Note:
When waves from two coherent sources superimpose, interference occurs. Where both waves interfere constructively, maximum is observed and where the waves interfere destructively minimum is obtained. Interference will be constructive or destructive depending on the path difference between the waves.