Question

A solid spherical ball is rolling without slipping down an inclined plane. The fraction of its total energy associated with the rotation is:
\[\begin{align}
  & \text{A}\text{. }\dfrac{2}{5} \\
 & \text{B}\text{. }\dfrac{2}{7} \\
 & \text{C}\text{. }\dfrac{3}{5} \\
 & \text{D}\text{. }\dfrac{3}{7} \\
\end{align}\]

Answer 1

Hint: We know the moment of inertia of solid spherical cell hence we know that solid spherical shell is rolling and sliding hence it will possess kinetic as well as rotational energy we know the moment of inertia so we can calculate rotational energy and total kinetic energy and we will take the given ratio.

Formula used:
$T=K.{{E}_{linear}}+K.{{E}_{rotational}}$
$K.{{E}_{rotational}}=\dfrac{1}{2}I{{\omega }^{2}}$
$K.{{E}_{linear}}=\dfrac{1}{2}M{{v}^{2}}$

Complete step by step answer:

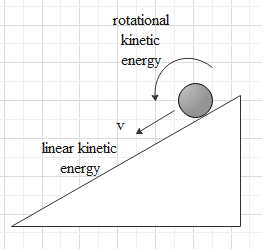
We know, moment of inertia, I of solid spherical shell of mass M about its central axis is given by
$I=\dfrac{2}{5}M{{R}^{2}}$
And we also know, kinetic energy in case of rotational dynamics is given by
$K.{{E}_{rotational}}=\dfrac{1}{2}I{{\omega }^{2}}$
Where $\omega $ is Angular velocity.
Now, kinetic energy for spherical ball,
$K.{{E}_{rotational}}=\dfrac{1}{2}\times \dfrac{2}{5}M{{R}^{2}}{{\omega }^{2}}=\dfrac{1}{5}M{{\left( R\omega \right)}^{2}}$
We know,
$v=\omega R$
So,
$K.{{E}_{rotational}}=\dfrac{1}{5}M{{v}^{2}}$
Linear kinetic energy
$K.{{E}_{linear}}=\dfrac{1}{2}M{{v}^{2}}$
So, total kinetic energy,
$T=K.{{E}_{linear}}+K.{{E}_{rotational}}$
Hence,
$\begin{align}
  & T=\dfrac{1}{2}M{{v}^{2}}+\dfrac{1}{5}M{{v}^{2}} \\
 & T=\dfrac{7}{10}M{{v}^{2}} \\
\end{align}$
Now, the fraction of its total energy associated with the rotation is
$=\dfrac{\dfrac{1}{5}M{{v}^{2}}}{\dfrac{7}{10}M{{v}^{2}}}=\dfrac{2}{7}$
Fraction of its total energy associated with the rotation is $\dfrac{2}{7}$.
Therefore the correct option is B.

Note:
When an object is rolling down a ramp, its energy is made up of three components:
\[mgh=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}I{{\omega }^{2}}\]
The first term is the potential energy; this is the energy it takes to lift the object up the ramp. This is equal to mgh, with m being the mass, g the acceleration due to gravity, and h the height of the ramp.
The second term is the translational kinetic energy; this is the energy it takes for the object to move down the ramp. This is equal to $\dfrac{1}{2}m{{v}^{2}}$, with m being the mass and v being the translational velocity.
The third term is the rotational kinetic energy; this is the energy it takes for the object to roll. This is equal to $\dfrac{1}{2}I{{\omega }^{2}}$, With I being the moment of inertia (the object’s resistance to being rotated) and ω being the angular velocity.
When an object is rolling such that a point on its edge has a velocity V, the angular velocity is given by (VR).