Question

A solid sphere of radius x cm is melted and cast into a shape of a solid cone of radius x cm. The height of the cone is:
A. 3x cm
B. x cm
C. 4x cm
D. 2x cm

Answer 1

Hint: At first, use the formula of volume of sphere which is \[\dfrac{4}{3}\pi {{r}^{3}}\] where r is radius, to find the volume of sphere. Then, find the volume of cone using formula, \[\dfrac{\pi {{r}^{2}}h}{3}\] where r is radius of cone and h is height. After that, compare both of the volumes to find the height.

Complete step-by-step answer:
In the question, a solid sphere of radius x is given. It is said that the given sphere was further melted and cast into a shape of solid cone of radius x. Now from this given information, we have to find the height of the cone.
Now, as we are told, the given solid sphere is melted and then again cast into a shape of a solid cone, so from this given information, we can say that, the volume of both the given sphere and cone is the same. Hence, from this we will find out the height.

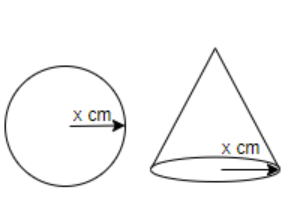
As the given radius of the sphere is x, so its volume can be find out using the formula \[\dfrac{4}{3}\pi {{r}^{3}}\] where r is the radius of the sphere. Here, the radius is x, so its volume will be $\dfrac{4}{3}\pi {{x}^{3}}$
Let’s take height of the cone as h and radius of base of cone is given as x, so we can find out using formula \[\dfrac{\pi {{r}^{2}}h}{3}\] where r is radius and h is height. Here, radius is x and height is h, so its volume will be \[\dfrac{\pi {{\left( x \right)}^{2}}\times h}{3}\Rightarrow \dfrac{\pi {{x}^{2}}h}{3}\]
Now, as we know that, the volume of both cone and sphere are same, so we can equate the volume of both cone and sphere, hence it can be written as \[\dfrac{4}{3}\pi {{x}^{3}}=\dfrac{\pi {{x}^{2}}h}{3}\]
Now, on further simplification we can write it as, \[4x=h\]
We can even say that the height of the cone is 4x.
Thus, the correct option is C.

Note: Generally in the question, if melted and cast processes are given then, one should first compare the volume. Also, one should be careful while writing formulas to avoid any mistakes. If one knows the formulas well, then they will be aware that the term 4 and h are the only different terms in respective formulas. Since the radius is the same in this question, one can mark 4x as the height of the cone by looking at the options.