Question

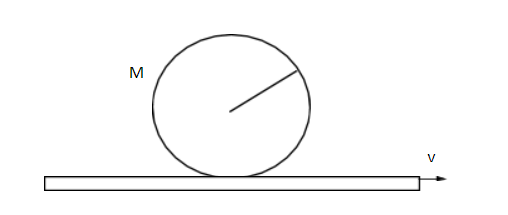
A solid sphere of mass m and radius R is gently placed on a conveyor belt moving with constant velocity v0. If coefficient of friction between belt and sphere is 2/7, the distance travelled by the centre of the sphere before it starts pure rolling is

A. $\dfrac{{{v_ \circ }^2}}{{7g}}$
B. $\dfrac{{2{v_ \circ }^2}}{{49g}}$
C. $\dfrac{{2{v_ \circ }^2}}{{5g}}$
D. $\dfrac{{2{v_ \circ }^2}}{{7g}}$

Answer 1

Hint: The translational and rotational motion is due to the friction between the belt and sphere. . For pure rolling, the velocity of the conveyor belt is to be equal to the velocity in a straight line and velocity due to rotation.

Complete step by step answer:
 A conveyor belt is moving with a constant velocity of v0. Now, a solid sphere of mass m and radius R is placed on it. A frictional force is acting between the sphere and belt. The coefficient of friction (μ) between belt and sphere is 2/7.
The translational motion exerted on the sphere is due to this frictional force. So,
$ma = \mu mg$
$a = \mu g$ [g is acceleration due to gravity]
$a = \dfrac{{2g}}{7}$
Now, the turning effect of the sphere is given by the formula τ = Iα and this turning effect is also due to the frictional force i.e., $F = \dfrac{\tau }{R}$
$\mu mg = \dfrac{{I\alpha }}{R}$ where I is moment of inertia about its centre
$\mu mg = \dfrac{{\dfrac{2}{5}m{R^2}\alpha }}{R}$ [$I = \dfrac{2}{5}m{R^2}$ about the diameter]
$\mu g = \dfrac{{2\alpha R}}{5}$
$\dfrac{2}{7}g = \dfrac{{2\alpha R}}{5}$
$\alpha = \dfrac{{\dfrac{2}{7}g}}{{\dfrac{{2R}}{5}}} = \dfrac{{2g}}{7} \times \dfrac{5}{{2R}} =
\dfrac{{5g}}{{7R}}$

When the sphere starts pure rolling, ${v_ \circ } = v + \omega R$
${v_0} = at + \left( {\alpha t} \right)R$ [$v = at,\omega = \alpha t$ where v is the velocity due to translational motion, ω is angular velocity due to rotational motion and t is the time taken to come to a start of rolling]
 ${v_0} = \left( {\dfrac{{2g}}{7}} \right)t + \left( {\dfrac{{5g}}{{7R}}} \right)tR$
${v_0} = \dfrac{{2gt}}{7} + \dfrac{{5gt}}{7} = \dfrac{{7gt}}{7}$
${v_0} = gt$
$t = \dfrac{{{v_0}}}{g}$
Substituting the value of t in equation, $S = ut + \dfrac{1}{2}a{t^2}$
$S = 0 \times t + \dfrac{1}{2} \times \dfrac{{2g}}{7} \times {\left( {\dfrac{{{v_0}}}{g}} \right)^2}$
$
  S = 0 + \dfrac{1}{2} \times \dfrac{{2g}}{7} \times \dfrac{{{v_0}^2}}{{{g^2}}} \\
  S = \dfrac{{{v_0}^2}}{{7g}} \\
$
Terms:
Torque: The turning effect of a force acting on a body (sphere) about an axis.
Moment of inertia: Sum of product of the masses of the particles and the square of their distances from the axis of rotation.

So, the correct answer is “Option A”.

Note:
The frictional force between the belt and sphere provides the necessary force required to rotate the sphere. As we have to calculate the distance travelled by the centre of the sphere. So, the moment of inertia is to be calculated along its diameter.