Question

A solid non-conducting sphere of radius $R$ has a uniform charge distribution of volume charge density, $\rho ={{\rho }_{0}}\dfrac{r}{R}$ where ${{\rho }_{0}}$ is a constant and $r$ is the distance from the center of the sphere. Show that:
(a) The total electric charge on the sphere is $Q=\pi {{\rho }_{0}}{{R}^{3}}$
(b) The electric field inside the sphere has a magnitude given by, $E=\dfrac{KQ{{r}^{2}}}{{{R}^{4}}}$.

Answer 1

Hint: The first part of the problem can be solved by considering the infinitesimal charge on the surface in spheres of radius $r$and thickness $dr$ and then integrating it for the whole sphere.
The second part of the problem can be solved by making use of Gauss’ Law which states that the total electric flux through a closed surface is equal to the charge enclosed within the surface divided by the permittivity. We will assume a sphere of radius r, find the charge enclosed in it and use gauss’ law to find the electric field from the electric flux.

Formula used:
$Q=\int\limits_{0}^{V}{\rho dV}$
where $Q$ is the total charge enclosed in the sphere, $\rho $ is the distribution of volume charge density and $dV$ is the volume of a thin strip of spherical shape at a radial distance $r$ from the center and having thickness $dr$.

$E.4\pi {{r}^{2}}=\dfrac{{{Q}_{enclosed}}}{{{\varepsilon }_{0}}}$ --(Gauss’ Law for a spherical surface)
where $E$ is the electric field in a sphere of radius $r$ due to the charge enclosed ${{Q}_{enclosed}}$ in it.

Complete step-by-step answer:
We are given a sphere of radius $R$ with uniform charge distribution and volume charge density as , $\rho ={{\rho }_{0}}\dfrac{r}{R}$ where ${{\rho }_{0}}$ is a constant and $r$ is the distance from the center of the sphere.
Thus, to find out the total charge enclosed in the sphere we will assume thin spherical strips inside the sphere at a radial distance r and thickness dr, find out its volume and find out the charge in it by the volume charge density given. Then we will integrate the result for $r=0$ to $r=R$ to get the charge enclosed in the whole sphere.

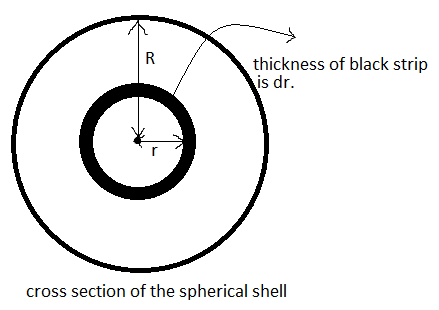
Therefore, mathematically,
$dQ=\rho dV$
$\therefore \int\limits_{0}^{Q}{dQ}=Q=\int\limits_{0}^{V}{\rho dV}$
Now, $dV=4\pi {{r}^{2}}dr$ --(since the surface area of the spherical strip will be $4\pi {{r}^{2}}$ ) $\therefore Q=\int\limits_{0}^{R}{\rho 4\pi {{r}^{2}}dr}$ Now, given $\rho ={{\rho }_{0}}\dfrac{r}{R}$, Therefore putting this value, we get, $Q=\int\limits_{0}^{R}{{{\rho }_{0}}\dfrac{r}{R}4\pi {{r}^{2}}dr}=\dfrac{4\pi {{\rho}_{0}}}{R}\int\limits_{0}^{R}{{{r}^{3}}dr=\dfrac{4\pi {{\rho }_{0}}}{R}\left[\dfrac{{{R}^{4}}}{4}-\dfrac{0}{4} \right]=\pi {{\rho }_{0}}{{R}^{3}}}$ --(1)
Hence, $Q=\pi {{\rho }_{0}}{{R}^{3}}$ --[Hence proved]
For, the second part of the question, we have to prove that The electric field inside the sphere has a magnitude given by, $E=\dfrac{KQ{{r}^{2}}}{{{R}^{4}}}$.
For this, we will use Gauss’ Law which states that the total electric flux through a closed surface is equal to the charge enclosed within the surface divided by the permittivity.
We will find the charge enclosed in a smaller sphere of radius $r$ using the same method as the first part and find out the electric field from the electric flux using the relation that
$E.4\pi {{r}^{2}}=\dfrac{{{Q}_{enclosed}}}{{{\varepsilon }_{0}}}$ --(Gauss’ Law for a spherical surface)--(2) where $E$ is the electric field in a sphere of radius $r$ due to the charge enclosed ${{Q}_{enclosed}}$ in it, and ${{\varepsilon }_{0}}$ is the permittivity of free space equal to $8.85\times {{10}^{-12}}{{m}^{-3}}k{{g}^{-1}}{{s}^{4}}{{A}^{2}}$
Hence, charge enclosed in the sphere of radius $r$ will be (proceeding the same way as in the first part of the question, that is, equation (1)),
${{Q}_{enclosed}}=\int\limits_{0}^{r}{{{\rho }_{0}}\dfrac{r}{R}4\pi {{r}^{2}}dr}=\dfrac{4\pi {{\rho }_{0}}}{R}\int\limits_{0}^{r}{{{r}^{3}}dr=\dfrac{4\pi {{\rho }_{0}}}{R}\left[ \dfrac{{{r}^{4}}}{4}-\dfrac{0}{4} \right]=\dfrac{\pi {{\rho }_{0}}{{r}^{4}}}{R}}$
Putting this in (2), we get,
$E.4\pi {{r}^{2}}=\dfrac{\pi {{\rho }_{0}}{{r}^{4}}}{R{{\varepsilon }_{0}}}$ $\therefore E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\times \pi {{\rho }_{0}}{{R}^{3}}\times \dfrac{{{r}^{2}}}{{{R}^{4}}}=\dfrac{KQ{{r}^{2}}}{{{R}^{4}}}$ --[Using (1) and since $\left( \because K=\dfrac{1}{4\pi {{\varepsilon }_{0}}} \right)$ where K is the universal electric constant.]
Hence (b) is also proved.

Note: One thing should be kept in mind by the students. The electric flux and hence the electric field on the left hand side in the mathematical expression of the Gauss’ law is due to all the charges inside and outside a closed surface however the charge on the right hand side of the equation is only the total value of the charge enclosed within the surface. Many questions are made upon this concept to confuse students, especially in competitive exams. Students should understand this concept properly.