Question

A solid metallic right circular cone 20cm high with vertical angle ${60^0}$ is cut into two parts at the middle point of its height by a plane parallel to the base. If the frustum, so obtained, be drawn into a wire of diameter $\dfrac{1}{{16}}cm,$ find the length of the wire.

Answer 1

Hint- In this question, we will use a simple approach that since we are cutting the right circular cone by the plane parallel to the base, we are getting a frustum. In the triangle so formed in the upper part of the cone, we will use the trigonometric ratios to find the smaller radius of the frustum and also the bigger radius of the frustum.

Complete step-by-step solution -

Now we will calculate the height of the frustum by simply dividing the height of the right circular cone by 2 because the plane is dividing at the middle point. After calculating all the parameters, just find the volume of the frustum. The wire is drawn using the frustum so since we are knowing the diameter of the wire. We will just equate the volumes of both to get the length of the wire which is a cylindrical one by equating both the equations.
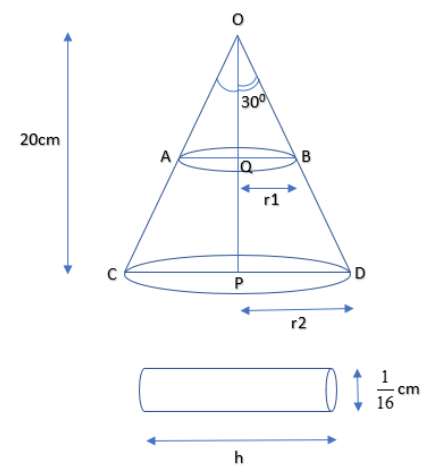
Let OCD be the metallic cone and ABCD be the required frustum.
Let OB = $r_1$, PD = $r_2$
Since, $\angle AOB = {60^0}$
so, \[\angle QOB = \dfrac{{\angle AOB}}{2} = \dfrac{{{{60}^0}}}{2} = {30^0}\]
Now, OP = 20cm and Q is the midpoint so, OQ = QP = 10cm.
In $\Delta OQB,$
$ \Rightarrow \tan {30^0} = \dfrac{{QB}}{{OQ}}$ as $\tan \theta = \dfrac{P}{B}$
We know that $\tan {30^0} = \dfrac{1}{{\sqrt 3 }}$
$ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{r_1}}{{10cm}}$
On cross multiplying, we get
$ \Rightarrow r_1 = \dfrac{{10}}{{\sqrt 3 }}cm$
In $\Delta OPD,$
$ \Rightarrow \tan {30^0} = \dfrac{{PD}}{{OP}}$ as $\tan \theta = \dfrac{P}{B}$
We know that $\tan {30^0} = \dfrac{1}{{\sqrt 3 }}$
$ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{r_2}}{{20cm}}$
On cross multiplying, we get
$ \Rightarrow r_2 = \dfrac{{20}}{{\sqrt 3 }}cm$
Now, we know that Volume of frustum
 $ = \dfrac{1}{3} \times \pi \times h \times \left( {{r_1}^2} + {{r_2}^2} +{ r_1 \times r_2} \right) = \dfrac{1}{3} \times \pi \times 10cm \times \left( {{{\left( {\dfrac{{10}}{{\sqrt 3 }}cm} \right)}^2} + {{\left( {\dfrac{{20}}{{\sqrt 3 }}cm} \right)}^2} + \dfrac{{10}}{{\sqrt 3 }}cm \times \dfrac{{20}}{{\sqrt 3 }}cm} \right)$
\[ = \dfrac{1}{3} \times \pi \times 10cm \times \left( {\dfrac{{100}}{3}c{m^2} + \dfrac{{400}}{3}c{m^2} + \dfrac{{200}}{3}c{m^2}} \right) = \dfrac{{10\pi }}{3}cm \times \dfrac{{700}}{3}c{m^2} = \dfrac{{7000\pi }}{9}c{m^3}\]
Now, since frustum is drawn into the wire so volume of the frustum is equal to the volume of the wire.
Now let us suppose the height of the wire be h
We have been given the diameter of the wire to be $\dfrac{1}{{16}}cm$
We know that radius is the half of diameter.
Let us suppose radius of the base of the wire be r
$r = \dfrac{{\left( {\dfrac{1}{{16}}} \right)}}{2}cm = \dfrac{1}{{32}}cm$
Now, volume of the cylindrical wire $ = \pi {r^2}h = \pi \times {\left( {\dfrac{1}{{32}}cm} \right)^2} \times h = \dfrac{{\pi h}}{{1024}}c{m^2}$
Since, the volume of the frustum is equal to the volume of the wire.
$ \Rightarrow \dfrac{{7000\pi }}{9}c{m^3} = \dfrac{{\pi h}}{{1024}}c{m^2}$
On cross multiplying we get,
$ \Rightarrow (7000 \times 1024)cm = 9h$
Divide both sides by 9 we get,
$ \Rightarrow \dfrac{{(7000 \times 1024)}}{9}cm = h$
or, $h = \dfrac{{(7000 \times 1024)}}{9}cm$
We know that $1cm = \dfrac{1}{{100}}m$
$ \Rightarrow h = \dfrac{{(7000 \times 1024)}}{9} \times \dfrac{1}{{100}}m = \dfrac{{(70 \times 1024)}}{9}m = 7964.44m$
Hence, the length of the wire so drawn is 7964.44m

Note- In such types of questions just keep in mind the basic formulas for calculation purposes. Volume of the frustum $ = \dfrac{1}{3} \times \pi \times h \times \left( {{r_1}^2} + {{r_2}^2} + {r_1 \times r_2} \right)$ and volume of the cylinder $ = \pi {r^2}h$ . Also keep in mind the various trigonometric ratios and their values at particular angles like $\tan {30^0} = \dfrac{1}{{\sqrt 3 }}$