Question

A solid metallic cylinder of base radius 3 cm and height 5 cm is melted to form cones each of height 1 cm and base radius 1mm. The number of cones is
A. 450
B. 1350
C. 4500
D. 13500

Answer 1

Hint: In this problem, first, we need to find out the volume of the cylinder and volume of one cone. Now, divide the volume of a cylinder by the volume of a cone to obtain the total number of cones.

Complete step-by-step solution:

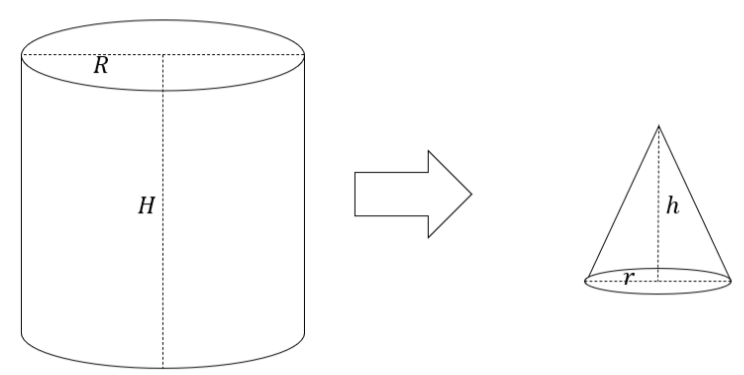
The formula for the volume \[V\] of the cylinder is shown below.
\[V = \pi {R^2}H\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,......\left( 1 \right)\]
Here, \[R\] is the radius of the cylinder, and \[H\] is the height of the cylinder.
Substitute, 3 for \[R\] and for \[H\] in equation (1) to obtain the volume of the cylinder.
\[\begin{gathered}
  \,\,\,\,\,\,\,V = \pi {\left( 3 \right)^2}\left( 5 \right) \\
   \Rightarrow V = \pi \left( 9 \right)\left( 5 \right) \\
   \Rightarrow V = 45\pi c{m^3} \\
\end{gathered}\]
The formula for the volume \[{V_1}\] of the cone is shown below.
\[{V_1} = \dfrac{1}{3}\pi {r^2}h\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,......\left( 2 \right)\]
Here, \[r\] is the radius of the base of the cone, and \[h\] is the height of the cone.
Convert, the unit of the radius of the cone into centimeters as shown below.
\[\begin{align}
  r = 1{\text{mm}} \\
  r = 0.1{\text{cm}} \\
\end{align}\]
Substitute, 0.1 for \[r\] and 1 for \[h\] in equation (2) to obtain the volume of the cone.

$ {V_1} = \dfrac{1}{3}\pi {\left( {0.1} \right)^2}\left( 1 \right) $
$\Rightarrow {V_1} = \dfrac{{0.01\pi }}{3}c{m^3} $
Now, the units of the volume of the cylinder and volume of the cone is same, so the ratio of the volume of cylinder to the volume of cone is unitless.
Divide, the volume of the cylinder by the volume of cones, to obtain the number of cones as shown below.
$ {\text{ Number of cones = }}\dfrac{{{\text{Volume of cylinder}}\left( V \right)}}{{{\text{Volume of cone}}\left( {{V_1}} \right)}} $
$\Rightarrow {\text{Number of cones = }}\dfrac{{45\pi }}{{\dfrac{{0.01\pi }}{3}}} $
$\Rightarrow {\text{Number of cones = }}\dfrac{{135}}{{0.01}} $
$\Rightarrow {\text{Number of cones = }}13500 $
Thus, the total number of cones is 13500, and hence, option (d) is the correct answer.

Note: When a solid melt, the volume of the solid remains constant. Convert, the radius of the cone into centimeters. The volume of the cylinder or cone represents its capacity. When two identities having the same units are divided the results are unitless.