Question

A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of \[\pi \].

Answer 1

Hint: The volume of a hemisphere with radius r is \[\dfrac{2}{3}\pi {r^3}\] and the volume of the cone with radius r and height h is \[\dfrac{1}{3}\pi {r^2}h\]. Find the volumes of hemisphere and cone separately and add them to get the required answer.

Complete step-by-step answer:
A hemisphere is half of the sphere cut by the plane passing through its center. The volume of the hemisphere is half of that of the sphere.
A hemisphere with radius r has a volume given as follows:
\[{V_H} = \dfrac{2}{3}\pi {r^3}...........(1)\]
A cone is a right angle triangle that is rotated with any one of its perpendicular sides as the axis in 3-dimensional space. The volume of the cone is one-third of the volume of the cylinder.
The volume of a cone of radius r and height h is given as follows:
\[{V_C} = \dfrac{1}{3}\pi {r^2}h...........(2)\]

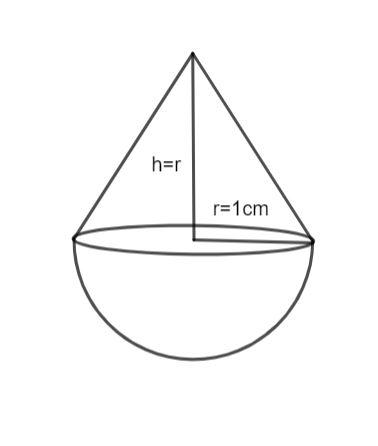
The solid in the given question is composed of a hemisphere and a cone. We can calculate its volume by calculating separately the volumes of cones and hemisphere and adding them.
The volume of the hemisphere of radius 1 cm is given by equation (1) as follows:
 \[{V_H} = \dfrac{2}{3}\pi {(1)^3}\]
\[{V_H} = \dfrac{2}{3}\pi c{m^3}\]
The volume of the cone of radius 1 cm and height 1 cm is given by equation (2) as follows:
\[{V_C} = \dfrac{1}{3}\pi {(1)^2}(1)\]
\[{V_C} = \dfrac{1}{3}\pi c{m^3}\]
Adding the two volumes, we have:
\[V = {V_H} + {V_C}\]
\[V = \dfrac{2}{3}\pi + \dfrac{1}{3}\pi \]
\[V = \pi c{m^3}\]
Hence, the volume of the solid is \[\pi \] cubic cm.

Note: The question is asked to find the volume of the solid in terms of \[\pi \], hence, leave the answer in terms of \[\pi \], if you evaluate, then the answer will be wrong.Students should remember formulas of volume of hemisphere and cone for solving these type of problems.