Question

A solid is in the shape of a bowl standing on a hemisphere with both their radii being equal to 12m and height of the bowl is 5m. Find the volume of the solid (use $\pi =3$)
\[\begin{align}
  & A.1018{{m}^{3}} \\
 & B.4176{{m}^{3}} \\
 & C.1028{{m}^{3}} \\
 & D.1308{{m}^{3}} \\
\end{align}\]

Answer 1

Hint: At first, find the volume of different shapes separately and then add them up using formula that, volume of cone is $\dfrac{\pi {{r}^{2}}h}{3}$ and that of hemisphere is $\dfrac{2}{3}\pi {{r}^{3}}$ where r is radius and h is height.

Complete step by step answer:
In the question we are given a solid with a hemisphere surmounted by a cone such that the diameter of the base shared by both the cone and hemisphere is 12m and the height of the cone is 5m.
Now, to find the total volume of the given solid, we find the volume separately and then sum it up to get the answer.
The figure of the solid is,

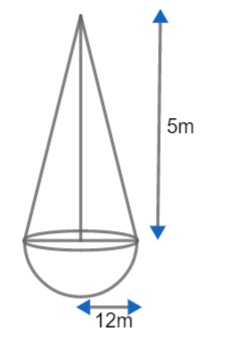
To find the volume, we will use a formula to find the volume of the cone which is $\dfrac{\pi {{r}^{2}}h}{3}$ where r is given radius and his height.
Now on substituting r as 12m and height as 5m we get:
\[\dfrac{\pi }{3}\times {{\left( 12 \right)}^{2}}\times 5\Rightarrow \dfrac{\pi }{3}\times 144\times 5\]
On substituting $\pi $ as 3 we get:
\[\dfrac{3}{3}\times 144\times 5\Rightarrow 720{{m}^{3}}\]
Now, to find the volume of the hemisphere whose radius is 12m we will use the formula $\dfrac{2}{3}\pi {{r}^{3}}$ where r is radius.
Now, on substituting r as 12m in formula we get:
\[\dfrac{2}{3}\times \pi \times 12\times 12\times 12\]
On substituting $\pi $ as 3 we get:
\[\dfrac{2}{3}\times 3\times 12\times 12\times 12\Rightarrow 3456{{m}^{3}}\]
So the total volume is \[\left( 720{{m}^{3}}+3456{{m}^{3}} \right)\Rightarrow 4176{{m}^{3}}\]
So the correct option is B.

Note:
Students while solving theory, generally miss out these formulas and make mistakes while doing calculation or leading with calculation of large numbers. So, they should be careful about it.