Question

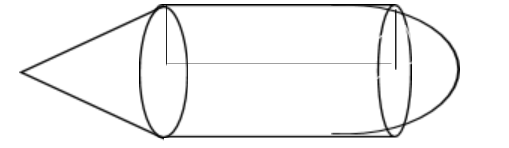
A solid is composed of a cylinder with a hemisphere at one end and a cone at the other end as shown in the figure. If the radius of each of these solids is 7 cm and the height of the cylinder is equal to slant height of the cone, find the total surface area of the solid if slant height is 4 cm.

Answer 1

Hint: To solve the question, we have to understand that not all the surface areas of the cylinder, cone and hemisphere include in the total surface of the solid.

Complete step-by-step answer:
Given
The radius of cylinder, cone, hemisphere are equal and the measurement is equal to 7 cm.
The height of the cylinder is equal to the slant height of the cone = 4 cm.
Let \[r,h,l\]be the radius of the solids, height of the cylinder and slant height of the cone respectively.
\[\Rightarrow r=\] 7 cm and \[h=l=\]4 cm.
The total surface area (TSA) of the solid is equal to the sum of curved surface areas of cylinder, cone and hemisphere of the given solid.
We know the formulae for Curved Surface Area (CSA) of the solids,
The curved surface area of cylinder \[=2\pi rh\]
The curved surface area of cone \[=\pi rl\]
The curved surface area of hemisphere \[=2\pi {{r}^{2}}\]
\[\Rightarrow \]The total surface area of the solid \[=2\pi rh+\pi rl+2\pi {{r}^{2}}\]
By substituting the values in the above equation, we get
TSA \[=\pi \left( 2\times 7\times 4+7\times 4+2\times {{7}^{2}} \right)\]
\[=\pi \left( 56+28+98 \right)\]
\[=182\pi c{{m}^{2}}\]
We know that \[\pi =3.14\]
TSA \[=182\times 3.14\] \[=571.48c{{m}^{2}}\]
\[\therefore \]The total surface area of the solid \[=571.48c{{m}^{2}}\].

Note: The possibility of mistake is not able to analyse that the total surface area of the solid is not the sum of TSA of the given solids instead it is CSA of the given solids. The other possible mistake is not applying the right CSA formulae for the given solids.