Question

A solid iron rectangular block of dimensions \[4.4m \times 2.6m \times 1m\] is cast into a hollow cylindrical pipe of internal radius 30 cm and the thickness 5 cm. Find the length of the pipe.

Answer 1

Hint: To find the length of the pipe we had to find the volume of the solid rectangular block i.e. \[l \times b \times h\] and then equate that with the volume of pipe i.e. \[\pi {r^2}h\] to get the length of the pipe.

Complete step-by-step answer:

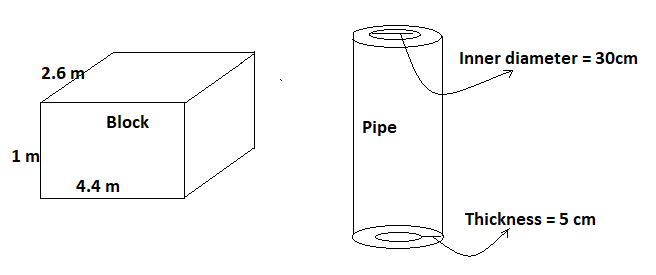
As we know that if any block is casted into a pipe then they both must have the same volume.
So, the volume of the rectangular block will be \[4.4 \times 2.6 \times 1 = 11.44{m^3}\].
Now according to the formula of volume of cylinder that is \[\pi {r^2}h\], where r is the radius and h is the height of the cylinder.
But the volume of the pipe will be equal to the volume of the outer cylinder minus the volume of the inner cylinder of the pipe.
As we know that the internal radius of the pipe is r = 30 cm = 0.3m (1m = 100 cm)
And the thickness of the pipe is 5 cm.
So, the outer radius of the pipe will be R = 30 + 5 = 35 cm = 0.35m (1m = 100 cm)
Let the length of the pipe be l metres.
So, volume of the pipe will be = \[\pi {R^2}h - \pi {r^2}h = \pi h\left( {{R^2} - {r^2}} \right)\]
As we know that the volume of pipe and block should be equal. So,
11.44 \[ = \pi h\left( {{{\left( {0.35} \right)}^2} - {{\left( {0.3} \right)}^2}} \right) = \pi h\left( {0.1225 - 0.09} \right) = 0.325\pi h\]
11.44 = \[0.325\pi h\]
Now dividing both sides of the above equation by \[0.325\pi \] and putting \[\pi \] = 3.14. We get,
h = \[\dfrac{{11.44}}{{0.325 \times 3.14}}\] = 11.2 m
Hence, the length of the cylindrical pipe will be equal to 11.2 metres.

Note: Whenever we come up with this type of problem then first, we have to find the volume of the block. Then after finding the inner and outer radius of the pipe we had to find the volume of the pipe by subtracting volume of inner cylinder of pipe from the volume of outer cylinder of the pipe and then equate that with the volume of block to get the required value of length of the pipe. This will be the easiest and efficient way to find the solution of the problem.