Question

A small particle of mass $ m $ moving inside a heavy, hollow and straight tube along the tube axis undergoes elastic collision at two ends. The tube has no friction and it is closed at one end by a flat surface while the other end is fitted with a heavy movable flat piston as shown in the figure, when the distance of the piston from the closed end is $ L = {L_0} $ the particle speed is $ v = {v_0} $ . The piston is moved inward at a very low speed such that $ V < < \dfrac{{dL}}{L}{v_0} $ . Where $ dL $ is an infinitesimal displacement of the piston.
Which of the following statements is correct?
A. After each collision with the piston, the particle speed increases by $ 2V $
B. If the piston moves inward by $ dL $ , the particle speed increases by $ 2V\dfrac{{dL}}{L} $
C. The particle’s kinetic energy increases by factor of $ 4 $ when the piston is moved inward from $ {L_0} $ to $ \dfrac{1}{2}{L_0} $
D. The rate at which the particle strikes at the piston is $ \dfrac{v}{L} $

Answer 1

Hint :In order to solve this question, we are going to see the conditions before and after the collision and the rate at which a particle hits the piston then, the speed of particle is found from the rate of change of velocity and afterwards the kinetic energies of a particle initially and finally.
The rate of change of velocity is
 $ \dfrac{{dv}}{{dt}} = f \times 2V $
Kinetic energy, $ K = \dfrac{1}{2} \times m \times {v^2} $
 $ m = mass \\
  v = velocity \\ $

Complete Step By Step Answer:
The inferences that can be drawn from the question
Piston before the collision

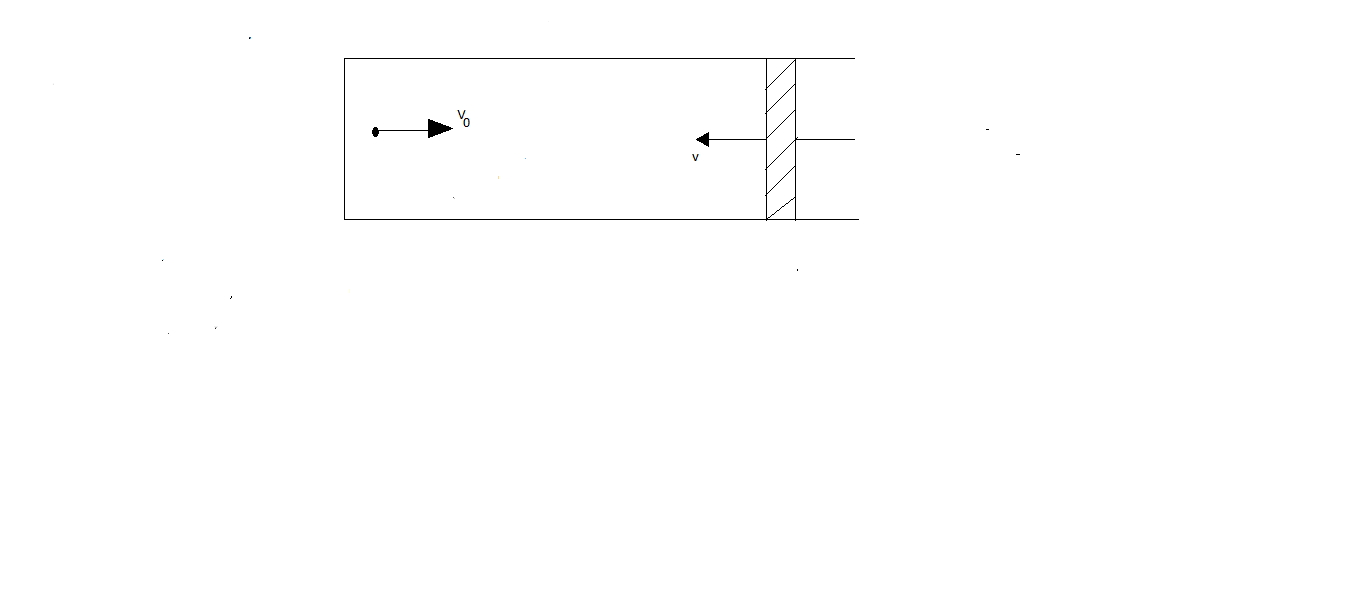
After the collision,

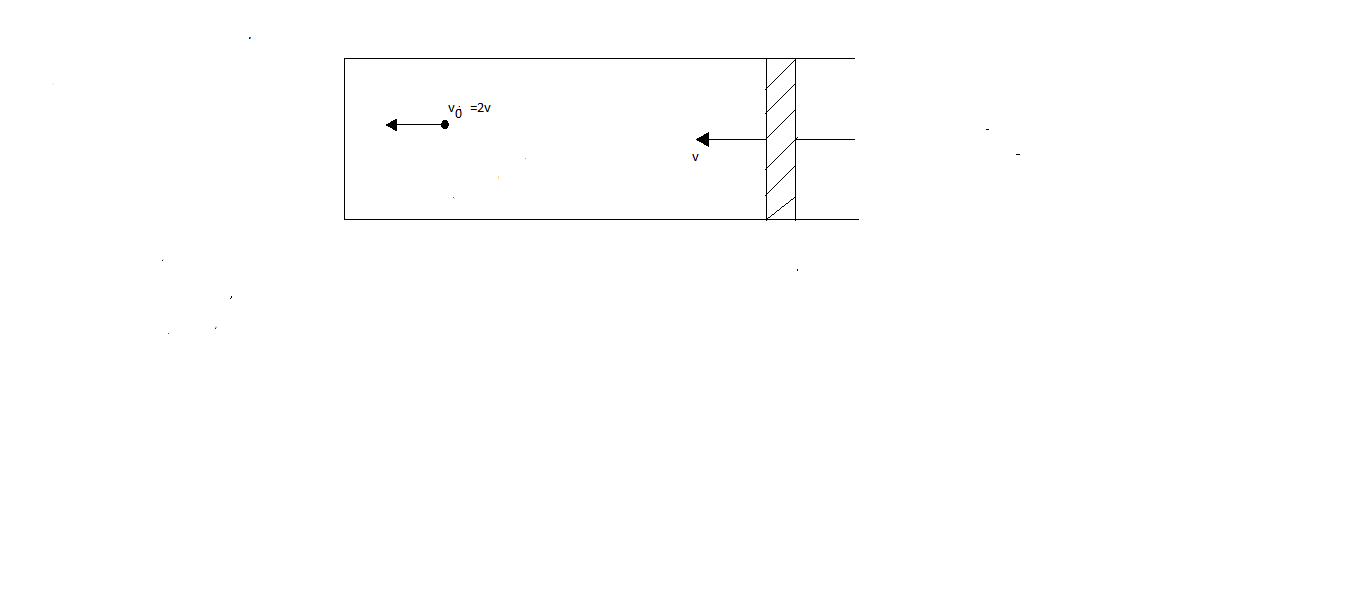
The rate at which the particle strikes the piston is given by
 $ = f = \dfrac{v}{{2x}} $
If $ x = L $ , then, $ f = \dfrac{v}{{2L}} $
The rate of the change of speed of particle is
 $ \dfrac{{dv}}{{dt}} = f \times 2V \\
  dv = \dfrac{v}{{2x}} \times 2Vdt \\
  dv = \dfrac{v}{{2x}} \times 2\left( { - dx} \right) \\ $
Now integrating to find the velocity,
 $ \Rightarrow \int\limits_{{v_0}}^v {\dfrac{{dv}}{v} = \int\limits_l^x {\dfrac{{ - dx}}{x}} } \\
   \Rightarrow \ln \dfrac{v}{{{v_0}}} = - \ln \dfrac{x}{l} \\
   \Rightarrow v = \dfrac{{{v_0}l}}{x} \\ $
Now, taking the case, $ x = \dfrac{{{L_0}}}{2} $
Then, if we find the velocity
 $ v = \dfrac{{{v_0}{L_0} \times 2}}{{{L_0}}} $
Now finding the kinetic energy at the value $ x = \dfrac{{{L_0}}}{2} $
 $ {K_f} = \dfrac{1}{2} \times m \times 4{v_0}^2 $
Kinetic energy at $ x = {L_0} $
 $ {K_i} = \dfrac{1}{2} \times m \times {v_0}^2 $
Therefore, the ratio of the kinetic energies is
 $ \dfrac{{{K_f}}}{{{K_i}}} = \dfrac{4}{1} = 4 $
Therefore, the options that are correct are A and C.

Note :
After each collision with the piston, the particles hit the piston with more and more energy that is , the particle speed increases by $ 2V $ and if we find the corresponding particle’s kinetic energy , it increases by factor of $ 4 $ when the piston is moved inward from $ {L_0} $ to $ \dfrac{1}{2}{L_0} $ .