Question

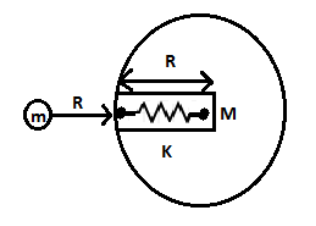
A small ball of mass ′ \[m\]′ is released at a height ′ \[R\]′ above the earth surface as shown in the given figure. If the maximum depth of the ball to which it goes is \[2R\] ​inside the earth through a narrow groove before coming to rest momentarily. The groove contains an ideal spring of spring constant \[K\] and natural length \[R\]. The value of \[K\], (\[R\] is the radius of earth and \[M\] is mass of the earth)

\[\begin{align}
  & A)\dfrac{3GMm}{{{R}^{3}}} \\
 & B)\dfrac{6GMm}{{{R}^{3}}} \\
 & C)\dfrac{9GMm}{{{R}^{3}}} \\
 & D)\dfrac{7GMm}{{{R}^{3}}} \\
\end{align} \]

Answer 1

Hint: Consider the law of conservation of energy to solve this question. Initially, the ball has gravitational potential energy. When the ball is released, as while falling down, it attains kinetic energy. Once it touches the spring, the spring compresses, due to which the ball attains elastic potential energy. When the ball is inside the groove, gravitational potential energy also acts on the ball. Hence, according to the law of conservation of energy, the initial energy on the ball and final energy on the ball are equal. Here, the initial gravitational potential energy is equal to the sum of final gravitational potential energy and the elastic potential energy. Using this we can find out the value of the spring constant.
Formula used:
\[{{\left( \text{Total energy} \right)}_{initial}}={{\left( \text{Total energy} \right)}_{final}}\]
\[{{\left( P.E \right)}_{initial}}=\dfrac{GMm}{2R}\]
\[\left( P.E \right)=\dfrac{-GMm}{{{R}^{3}}}\left( \dfrac{3{{R}^{2}}}{2}-\dfrac{{{r}^{2}}}{2} \right)\]
\[{{E}_{P.E}}=\dfrac{1}{2}K{{x}^{2}}\]

Complete step-by-step solution:

Given,
 \[M\] is the mass of the earth
\[m\] is the mass of the ball
\[R\] is the distance from the initial position of the ball to the earth’s surface, which is the same as the radius of the earth.
Applying conservation energy, \[{{\left( \text{Total energy} \right)}_{initial}}={{\left( \text{Total energy} \right)}_{final}}\]
Initially, the ball has a gravitational potential energy and at the final position it has elastic potential energy and final gravitational potential energy. Then,
\[\text{Initial P}\text{.E= Final P}\text{.E+ elastic P}\text{.E}\] ---------------(1)
Initial gravitational potential energy of the ball is given by,
\[{{\left( P.E \right)}_{initial}}=\dfrac{-GMm}{2R}\] -------------- (2)
Where,
\[2R\] is the distance from the initial position of the ball to the center of the earth
\[G\] is the gravitational constant.
At any point inside a sphere, the gravitational potential energy is given by;
\[\left( P.E \right)=\dfrac{-GMm}{{{R}^{3}}}\left( \dfrac{3{{R}^{2}}}{2}-\dfrac{{{r}^{2}}}{2} \right)\]
Where,
\[r\] is the distance of the point to the center of the sphere.
Then, final gravitational potential energy of the ball is given by,
\[{{\left( P.E \right)}_{final}}=\dfrac{-GMm}{{{R}^{3}}}\left( \dfrac{3{{R}^{2}}}{2}-{{\left( \dfrac{R}{2} \right)}^{2}}\dfrac{1}{2} \right)=\dfrac{-GMm}{{{R}^{3}}}\left( \dfrac{3{{R}^{2}}}{2}-\dfrac{{{R}^{2}}}{8} \right)\]
Where,
\[\dfrac{R}{2}\] is the distance from the center of the earth to the final position of the ball.
\[\Rightarrow {{\left( P.E \right)}_{final}}=\dfrac{-GMm}{{{R}^{3}}}\times {{R}^{2}}\left( \dfrac{12-1}{8} \right)=\dfrac{-GMm}{R}\times \dfrac{11}{8}\] ------------------(3)
Now, let’s find the elastic potential energy due to spring.
We have,
\[{{E}_{P.E}}=\dfrac{1}{2}K{{x}^{2}}\]
Where,
\[x\] is the displacement of the spring from the natural length.
\[K\] is the spring constant.
Then,
\[{{E}_{P.E}}=\dfrac{1}{2}K{{\left(\dfrac{R}{2}\right)}^{2}}=\dfrac{1}{8}K{{R}^{2}}\] ------(4)
Here, \[\dfrac{R}{2}\] is the distance from the earth’s surface to the final position of the ball.
Then,
Substitute 2, 3 and 4 in equation 1, we get,
\[\Rightarrow \dfrac{-GMm}{2R}=\dfrac{-11}{8}\dfrac{GMm}{R}+\dfrac{1}{8}K{{R}^{2}}\]
\[\Rightarrow \dfrac{GMm}{R}\left( \dfrac{11}{8}-\dfrac{1}{2} \right)=\dfrac{1}{8}K{{R}^{2}}\]
\[\Rightarrow \dfrac{-GMm}{R}\left( \dfrac{11-4}{8} \right)=\dfrac{1}{8}K{{R}^{2}}\]
\[\Rightarrow \dfrac{7GMm}{R}=K{{R}^{2}}\]
\[\Rightarrow K=\dfrac{7GMm}{{{R}^{3}}}\]
The answer is option D.

Note: The gravitational constant is the proportionality constant which is used in Newton’s Law of gravitation, and is denoted by G, with a value \[G\text{ }=~6.673\times {{10}^{-11}}~N\text{ }{{m}^{2}}~k{{g}^{-2}}\]. It is different from \[g\], which denotes the acceleration due to gravity.