Question

A siphon is a device for removing liquid from a container that is not to be tilted. It operates as shown in fig. The tube must initially be filled, but once this has been done, the liquid flows until its level drops below the tube opening at A. Take liquid as water and neglect its viscosity.
Given atmospheric pressure $ ={{10}^{5}}Pa $ and density of water $ {{10}^{3}} $ $ kg/{{m}^{3}} $ and acceleration due to gravity is 10 $ m/{{s}^{2}} $ . Maximum possible value of $ {{h}_{2}} $ for siphon to work is (approximately):

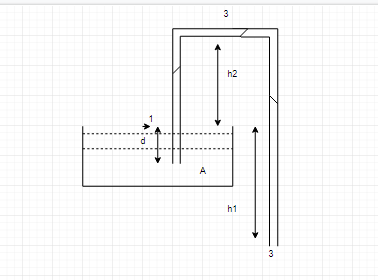
A: 20 m
B: 10 m
C: 5 m
D: for any value.

Answer 1

Hint: The device shown is a very common phenomenon that we are observing in our daily lives. Once, the liquid starts coming it continues until all the liquid from the container becomes empty. This flow of water happens due to the difference of pressure at the two ends of the pipe. We know the pressure difference led to many phenomena like lift in an airplane, etc.

Formula used: We make use of Bernoulli’s theorem to solve this problem.
 $ P+\dfrac{\rho {{v}^{2}}}{2}+\rho gh=k $ , where k is a constant.

Complete step by step solution:

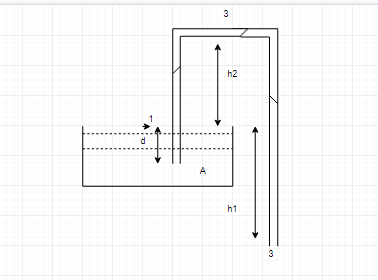
Applying Bernoulli's theorem at points $ 1 $ and $ 2 $ the height is being measured from the point $ 1 $ only, and the velocity of the liquid is zero at point $ 1 $ because the liquid is at rest. So,
 $ {{P}_{1}}+\dfrac{\rho {{v}_{1}}^{2}}{2}+\rho g{{h}_{1}}={{P}_{2}}+\dfrac{\rho {{v}_{2}}^{2}}{2}+\rho g{{h}_{2}} \\
\Rightarrow {{P}_{1}}+0+0={{P}_{2}}+\dfrac{\rho {{v}_{2}}^{2}}{2}+\rho g{{h}_{2}} \\
\Rightarrow {{P}_{1}}-{{P}_{2}}-\rho g{{h}_{2}}=\dfrac{\rho {{v}_{2}}^{2}}{2} \\
\Rightarrow v_{2}^{2}=\dfrac{2({{P}_{1}}-{{P}_{2}}-\rho g{{h}_{2}})}{\rho } \\
\therefore {{v}_{2}}=\sqrt{\dfrac{2({{P}_{1}}-{{P}_{2}}-\rho g{{h}_{2}})}{\rho }} \\ $
So, we have found out the velocity of the liquid at point $ 2 $ , but for maximum possible height, the velocity at that height must be equal to zero, thus,
 $ {{v}_{2}}=\sqrt{\dfrac{2({{P}_{1}}-{{P}_{2}}-\rho g{{h}_{2}})}{\rho }} \\
\Rightarrow \sqrt{\dfrac{2({{P}_{1}}-{{P}_{2}}-\rho g{{h}_{2}})}{\rho }}=0 \\
\Rightarrow {{P}_{1}}-{{P}_{2}}-\rho g{{h}_{2}}=0 \\
\Rightarrow \rho g{{h}_{2}}={{P}_{1}}-{{P}_{2}} \\
\Rightarrow {{h}_{2}}=\dfrac{{{P}_{1}}-{{P}_{2}}}{\rho g} \\ $
But the pressure, $ {{P}_{2}}=0 $
Thus, $ {{h}_{2}}=\dfrac{{{P}_{1}}}{\rho g} $ , putting the values of atmospheric pressure, acceleration due to gravity and density we get,
 $ \therefore {{h}_{2}}=\dfrac{{{10}^{5}}}{1000\times 10}=10m $
So, the correct option is (B).

Note:
Sometimes these kinds of problems are also solved using Pascal's law of pressure. Pascal law states that pressure remains the same at the same horizontal level in a liquid. Both the columns are exposed to the atmosphere and the height of the liquid is also given. But that way the problem becomes too complex and that’s why we have invoked Bernoulli's principle here.