Question

A simple pendulum of length $1m$ has a bob of mass $100 g$ . It is displaced through an angle of $60^\circ $ from the vertical and then released. Find out K.E of bob when it passes through mean position.
(A) $0.12 J$
(B) $0.24 J$
(C) $0.36 J$
(D) $0.55 J$

Answer 1

Hint: Energy obtained by a body due to the position it had occupied is called potential energy. When the body is in movement, then, the possessing energy is called kinetic energy. For a simple pendulum when the bob reaches the mean position, its potential energy will get converted to its kinetic energy.

Complete step by step answer:
Given that the mass of the bob of the pendulum is $100\;{\rm{g}}$. Converting the grams into kilograms by dividing the grams by $1000$, we have,
$
m = 100\;{\rm{g}}\\
\Rightarrow m = \dfrac{{100}}{{1000}}\;{\rm{kg}}\\
\Rightarrow m = 0.1\;{\rm{kg}}
$
It is also given that the pendulum with length $1\;{\rm{m}}$ is displaced through an angle of $60^\circle $ from the vertical. We can express this as in the figure,

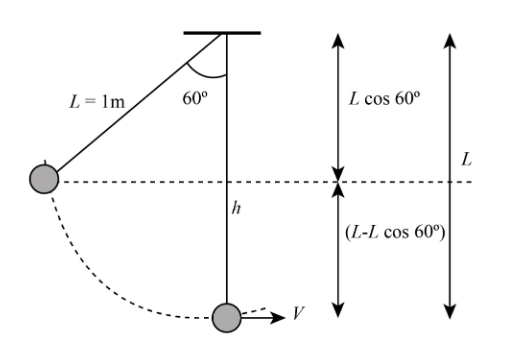
 That is here the length $l = 1\;{\rm{m}}$ and the angle $\theta = 60^\circ $.now we have the equation for the total length of the pendulum as,$l = l\cos \theta + h$, where $h$ is the height of pendulum. It is the height upto which the pendulum rises. Thus we have the formula for height as,
$
l = l\cos \theta + h\\
\Rightarrow h = l - l\cos \theta \\
\Rightarrow h = l(1 - \cos \theta )
$
Thus substituting for $l$ and $\theta $ ,
\[
h = 1(1 - \cos 60^\circ )\\
\Rightarrow h = 1\left( {1 - 0.5} \right)\\
\Rightarrow h = 0.5\;{\rm{m}}
\]
Since $\cos 60^\circ = \dfrac{1}{2}$.
The potential energy is calculated as, $PE = mgh$, where $m$ is the mass, $g$ is the acceleration due to gravity, and $h$ is the height.
Taking $g = 10\;{\rm{m/s}}$, and substituting $0.1\;{\rm{kg}}$ for $m$ and $0.5\;{\rm{m}}$ for $h$ , the potential energy of the pendulum is,
$
PE = 0.1\;{\rm{kg}} \times 10\;{\rm{m/s}} \times 0.5\;{\rm{m}}\\
\therefore PE{\rm{ = 0}}{\rm{.55}}\;{\rm{J}}
$
When the pendulum is released and reaches the mean position, the potential energy possessed is converted to the kinetic energy. Therefore the kinetic energy of bob when it passes through the mean position is $0.55\;{\rm{J}}$.
Therefore the correct answer is option (D) $0.55\;{\rm{J}}$.

Note: When the bob is at a height, it poses a potential energy by virtue of its position. When it is released, energy is required to change the position. This energy due to the movement is called kinetic energy. The stored potential energy is then converted to kinetic energy for the movement.